题目内容
4.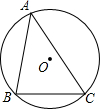 如图,半径为2的⊙O中,弦BC=2$\sqrt{3}$,A是优弧BC上的一个动点,P点是△ABC的内心,经过B、C、P三点作⊙M,当点A运动时,⊙M的半径( )
如图,半径为2的⊙O中,弦BC=2$\sqrt{3}$,A是优弧BC上的一个动点,P点是△ABC的内心,经过B、C、P三点作⊙M,当点A运动时,⊙M的半径( )| A. | 发生变化,随A位置决定 | B. | 不变,等于2 | ||
| C. | 有最大值为2$\sqrt{3}$ | D. | 有最小值为1 |
分析 作直径BD,由圆周角定理得出∠BCD=90°,∠BAC=∠D,由三角函数求出∠BAC=∠D=60°,得出∠BOC=2∠BAC=120°,∠ABC+∠ACB=120°,由内心的性质得出∠PBC+∠PCB=60°,由三角形内角和定理求出∠BPC=120°=∠BOC,证出点O在⊙M上,延长OM=CM,证出$\widehat{BM}=\widehat{CM}$,得出∠BOM=∠COM=60°,得出△OCM是等边三角形,即可得出结论.
解答 解:作直径BD,连接CD,OC,BM,CM,OM,如图所示: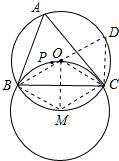
则∠BCD=90°,∠BAC=∠D,
∴sinD=$\frac{BC}{BD}=\frac{2\sqrt{3}}{4}$=$\frac{\sqrt{3}}{2}$,
∴∠BAC=∠D=60°,
∴∠BOC=2∠BAC=120°,∠ABC+∠ACB=120°,
∵P点是△ABC的内心,
∴∠PBC+∠PCB=$\frac{1}{2}$(∠ABC+∠ACB)=60°,
∴∠BPC=120°=∠BOC,
∴点O在⊙M上,
∴OM=CM,
∵BM=CM,
∴$\widehat{BM}=\widehat{CM}$,
∴∠BOM=∠COM=60°,
∴△OCM是等边三角形,
∴CM=OC=2,
即⊙M的半径不变,等于2.
故选:B.
点评 本题考查了三角形的内切圆与内心、三角函数的运用、圆周角定理、三角形内角和定理、等边三角形的判定与性质以及圆心角、弧、弦之间的关系等知识;本题综合性强,有一定难度.

练习册系列答案
相关题目
15.已知:⊙O是△ABC的外接圆,∠OAB=40°,则∠ACB的大小为( )
| A. | 20° | B. | 50° | C. | 20°或160° | D. | 50°或130° |
12.设2+$\sqrt{3}$的整数部分用a表示,小数部分用b表示,4-$\sqrt{3}$的整数部分用c表示,小数部分用d表示,则$\frac{b+d}{ac}$的值为( )
| A. | $\frac{1}{8}$ | B. | $\frac{1}{6}$ | C. | $\frac{5}{6}$ | D. | $\frac{1}{3}$($\sqrt{3}$-1) |
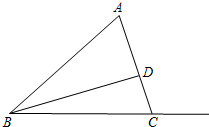 已知:△ABC中,AB=13,AC=9,BC=4$\sqrt{10}$,BD⊥AC于D.
已知:△ABC中,AB=13,AC=9,BC=4$\sqrt{10}$,BD⊥AC于D. 如图,△ABC为正三角形,点B、C、D、E在同一直线上,且CG=CD=DF=DE,则∠E=15°.
如图,△ABC为正三角形,点B、C、D、E在同一直线上,且CG=CD=DF=DE,则∠E=15°. 已知一次函数y=2x-k与反比例函数y=$\frac{k+2}{x}$的图象相交于A和B两点,如果有一个交点A的横坐标为3,
已知一次函数y=2x-k与反比例函数y=$\frac{k+2}{x}$的图象相交于A和B两点,如果有一个交点A的横坐标为3,