题目内容
15.已知:⊙O是△ABC的外接圆,∠OAB=40°,则∠ACB的大小为( )| A. | 20° | B. | 50° | C. | 20°或160° | D. | 50°或130° |
分析 由OA=OB,可求得∠OBA=∠OAB=40°,继而求得∠AOB的度数,然后由圆周角定理,求得答案.
解答 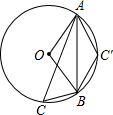 解:∵OA=OB,
解:∵OA=OB,
∴∠OBA=∠OAB=40°,
∴∠AOB=180°-∠OAB-∠OBA=100°,
∴∠ACB=$\frac{1}{2}$∠AOB=50°.
当点C在点C′的位置时,∠AC′B=180°-50°=130°.
故选D.
点评 本题考查的是圆周角定理,根据题意画出图形,利用数形结合求解是解答此题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
7.下列图形中,轴对称图形的个数为( )


| A. | 1个 | B. | 2 个 | C. | 3个 | D. | 4个 |
4.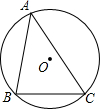 如图,半径为2的⊙O中,弦BC=2$\sqrt{3}$,A是优弧BC上的一个动点,P点是△ABC的内心,经过B、C、P三点作⊙M,当点A运动时,⊙M的半径( )
如图,半径为2的⊙O中,弦BC=2$\sqrt{3}$,A是优弧BC上的一个动点,P点是△ABC的内心,经过B、C、P三点作⊙M,当点A运动时,⊙M的半径( )
 如图,半径为2的⊙O中,弦BC=2$\sqrt{3}$,A是优弧BC上的一个动点,P点是△ABC的内心,经过B、C、P三点作⊙M,当点A运动时,⊙M的半径( )
如图,半径为2的⊙O中,弦BC=2$\sqrt{3}$,A是优弧BC上的一个动点,P点是△ABC的内心,经过B、C、P三点作⊙M,当点A运动时,⊙M的半径( )| A. | 发生变化,随A位置决定 | B. | 不变,等于2 | ||
| C. | 有最大值为2$\sqrt{3}$ | D. | 有最小值为1 |
5.下列方程中,解是x=2的是( )
| A. | x+4=2 | B. | 2x-3=2 | C. | x-3=-1 | D. | $\frac{1}{2}$x+1=3 |
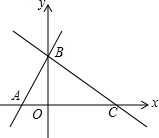 如图,一次函数y=(m-1)x+4的图象与x轴的负半轴相交于点A,与y轴相交于点B,且△OAB面积为4.
如图,一次函数y=(m-1)x+4的图象与x轴的负半轴相交于点A,与y轴相交于点B,且△OAB面积为4.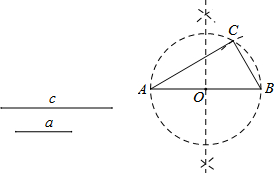 阅读下面材料:
阅读下面材料: 在平面直角坐标系xOy中,抛物线y=x2+bx+c经过点A(-1,t),B(3,t),与y轴交于点C(0,-1).一次函数y=x+n的图象经过抛物线的顶点D.
在平面直角坐标系xOy中,抛物线y=x2+bx+c经过点A(-1,t),B(3,t),与y轴交于点C(0,-1).一次函数y=x+n的图象经过抛物线的顶点D.