题目内容
15.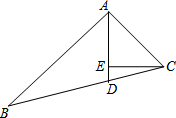 如图,在△ABC中,AD平分∠BAC,CE⊥AD,垂足为E,∠ACE,∠B,∠ECD之间的数量关系是( )
如图,在△ABC中,AD平分∠BAC,CE⊥AD,垂足为E,∠ACE,∠B,∠ECD之间的数量关系是( )| A. | 2∠ACE=∠B+∠ECD | B. | ∠ACE=∠B+∠ECD | C. | ∠ACE=∠B+2∠ECD | D. | ∠ACE=2(∠B+∠ECD) |
分析 延长CE交AB于F,求出∠AEC=∠AEF,∠FAE=∠CAE,根据ASA证△FAE≌△CAE,推出∠ACE=∠AFC,根据三角形外角性质得出∠AFC=∠B+∠ECD,代入求出即可.
解答  证明:延长CE交AB于F,
证明:延长CE交AB于F,
∵CE⊥AD,
∴∠AEC=∠AEF,
∵AD平分∠BAC,
∴∠FAE=∠CAE,
在△FAE和△CAE中,
$\left\{\begin{array}{l}{∠FAE=∠CAE}\\{AE=AE}\\{∠AEF=∠AEC}\end{array}\right.$,
∴△FAE≌△CAE(ASA),
∴∠ACE=∠AFC,
∵∠AFC=∠B+∠ECD,
∴∠ACE=∠B+∠ECD.
故选B.
点评 本题考查了全等三角形的性质和判定,三角形的外角性质等知识点,关键是作辅助线后求出∠AFC=∠ACE.

练习册系列答案
相关题目
10.二次函数y=ax2+bx+c的部分对应值如下表:
二次函数y=ax2+bx+c图象的对称轴为x=2,x=-1对应的函数值y=-22.
| x | … | -3 | -2 | 0 | 1 | 3 | 5 | … |
| y | … | -54 | -36 | -12 | -6 | -6 | -22 | … |
5.下列运算中,正确的是( )
| A. | (-3)2=-9 | B. | -22=4 | C. | $5÷\frac{1}{6}×6=5÷1=5$ | D. | 0$-(-\frac{1}{5})=\frac{1}{5}$ |
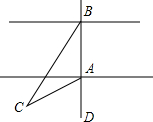 一次数学实践活动的内容是测量河宽,如图,即测量A,B之间的距离.同学们想出了许多方法,其中小聪的方法是:从点A出发,沿着与直线AB成60°角的AC方向前进至C,在C处测得∠C=30°,量出AC的长,它就是河宽(即A,B之间的距离),这个方法正确吗?请说明理由.
一次数学实践活动的内容是测量河宽,如图,即测量A,B之间的距离.同学们想出了许多方法,其中小聪的方法是:从点A出发,沿着与直线AB成60°角的AC方向前进至C,在C处测得∠C=30°,量出AC的长,它就是河宽(即A,B之间的距离),这个方法正确吗?请说明理由.