题目内容
11. 某生活小区的居民筹集资金1600元,计划在一块上,下两底分别为10m,20m的梯形空地种植花木.
某生活小区的居民筹集资金1600元,计划在一块上,下两底分别为10m,20m的梯形空地种植花木.(1)如图,他们在△AMD和△BMC地带上种植太阳花,当△AMD地带种满花后(图中阴影部分),共花了160元,请计算种满△BMC地带所需的费用;
(2)若其余地带要种的花卉,有玫瑰花和茉莉花和太阳花三种供选,单价分别为12元/m2,10元/m2,8元/m2,怎样安排栽种面积?请你作出决策.
分析 (1)证明△AMD∽△BMC,利用相似三角形的性质得$\frac{{S}_{△AMD}}{{S}_{△BMC}}$=($\frac{AD}{BC}$)2=$\frac{1}{4}$,于是得到种满△BMC地带所需的费用为△AMD地带种植费用的4倍;
(2)先计算出S△AMD=20(m2),则S△BMC=80,再根据相似三角形的性质得$\frac{DM}{CM}$=$\frac{AM}{BM}$=$\frac{AD}{BC}$=$\frac{1}{2}$,所以S△ACM=S△BDM=2S△AMD=40,然后分别讨论,使总费用不超过1600元即可.
解答 解:(1)∵AD∥BC,
∴△AMD∽△BMC,
∴$\frac{{S}_{△AMD}}{{S}_{△BMC}}$=($\frac{AD}{BC}$)2=($\frac{10}{20}$)2=$\frac{1}{4}$,
即S△BMC=4S△AMD,
∵△AMD地带种满花后(图中阴影部分),共花了160元,
∴种满△BMC地带所需的费用=4×160=640(元);
(2)∵种太阳花的单价为8元/m2,而△AMD地带种满花后(图中阴影部分),共花了160元,
∴S△AMD=$\frac{160}{8}$=20(m2),
∴S△BMC=80,
∵△AMD∽△BMC,
∴$\frac{DM}{CM}$=$\frac{AM}{BM}$=$\frac{AD}{BC}$=$\frac{10}{20}$=$\frac{1}{2}$,
∴S△ACM=S△BDM=2S△AMD=40,
当△ACM和△BDM都种玫瑰花,则费用为12×(40+40)=960,而△BMC和△AMD种花的费用为160+640=800(元),此时960+800>1600;
当△ACM和△BDM都种茉莉花,则费用为10×(40+40)=800,而△BMC和△AMD种花的费用为160+640=800(元),此时800+800=1600;
当△ACM和△BDM都种太阳花,则费用为8×(40+40)=640,而△BMC和△AMD种花的费用为160+640=800(元),此时640+800<1600;
当△ACM种玫瑰花和△BDM种太阳花,则费用为12×40+8×40=800,而△BMC和△AMD种花的费用为160+640=800(元),此时800+800=1600;
当△ACM种玫瑰花和△BDM都种茉莉花,则费用为12×40+10×40=880,而△BMC和△AMD种花的费用为160+640=800(元),此时880+800>1600;
所以可以这样安排:方案一:△AMD和△BMC地带上种植太阳花后,△ACM和△BDM都种茉莉花;方案二::△AMD和△BMC地带上种植太阳花后,△ACM和△BDM都种太阳花;方案三:△ACM种玫瑰花和△BDM种太阳花.
点评 本题考查了相似三角形的应用:先构建相似三角形,然后利用相似三角形的性质即相似三角形的对应边的比相等和相似三角形面积的比等于相似比进行计算.

| A. | 中国海洋面积是299.7万平方公里 | |
| B. | 中国老龄人口2050年将达峰值4.37亿 | |
| C. | 某校七年级(1)班有42人 | |
| D. | 《西游记》中孙悟空的本领真大,一个跟斗翻10万8千里 |
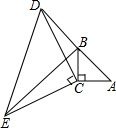 如图,在△ABC中,∠ACB=90°,AC=BC,延长AB至点D,使DB=AB,连接CD,以CD为直角边作等腰直角三角形CDE,其中∠DCE=90°,连接BE.
如图,在△ABC中,∠ACB=90°,AC=BC,延长AB至点D,使DB=AB,连接CD,以CD为直角边作等腰直角三角形CDE,其中∠DCE=90°,连接BE.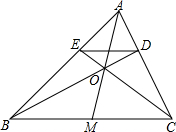 已知:如图,在△ABC中,AM是边BC的中线,O为AM上的任意一点,BO的延长线交AC于点D,CO的延长线交AB于点E,求证:ED∥BC.
已知:如图,在△ABC中,AM是边BC的中线,O为AM上的任意一点,BO的延长线交AC于点D,CO的延长线交AB于点E,求证:ED∥BC.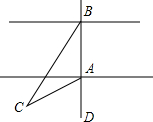 一次数学实践活动的内容是测量河宽,如图,即测量A,B之间的距离.同学们想出了许多方法,其中小聪的方法是:从点A出发,沿着与直线AB成60°角的AC方向前进至C,在C处测得∠C=30°,量出AC的长,它就是河宽(即A,B之间的距离),这个方法正确吗?请说明理由.
一次数学实践活动的内容是测量河宽,如图,即测量A,B之间的距离.同学们想出了许多方法,其中小聪的方法是:从点A出发,沿着与直线AB成60°角的AC方向前进至C,在C处测得∠C=30°,量出AC的长,它就是河宽(即A,B之间的距离),这个方法正确吗?请说明理由.