题目内容
17.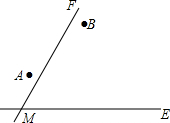 两个城镇A、B与两条公路ME,MF位置如图所示,其中ME是东西方向的公路.现电信部门需在C处修建一座信号发射塔,要求发射塔到两个城镇A、B的距离必须相等,到两条公路ME,MF的距离也必须相等,且在∠FME的内部.
两个城镇A、B与两条公路ME,MF位置如图所示,其中ME是东西方向的公路.现电信部门需在C处修建一座信号发射塔,要求发射塔到两个城镇A、B的距离必须相等,到两条公路ME,MF的距离也必须相等,且在∠FME的内部.(1)点C应选在何处?请在图中,用尺规作图找出符合条件的点C.(不写已知、求作、作法,只保留作图痕迹)
(2)点C到公路ME的距离为2km,设AB的垂直平分线交ME于点N,点M处测得点C位于点M的北偏东60°方向,在N处没得点C位于点N的北偏西45°方向,求MN的长(结果保留根号)
分析 (1)到城镇A、B距离相等的点在线段AB的垂直平分线上,到两条公路距离相等的点在两条公路所夹角的角平分线上,分别作出垂直平分线与角平分线,它们的交点即为所求作的点C;
(2)作CD⊥MN于点D.由三角函数得出MD=$\sqrt{3}$CD,DN=CD,于是得到结论.
解答 解:(1)如图所示,点C即为所求;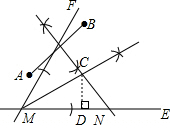
(2)作CD⊥MN于点D,
由题意得:∠CMN=30°,∠CND=45°,
∵在Rt△CMD中,$\frac{CD}{MD}$=tan∠CMN,
∴MD=$\frac{2}{\frac{\sqrt{3}}{3}}$=2$\sqrt{3}$;
∵在Rt△CND中,$\frac{CD}{DN}$=tan∠CNM,
∴ND=CD=2,
∵MN=DM+DN=2$\sqrt{3}$+2km,
点评 本题考查了解直角三角形的应用、作图-设计;熟练掌握基本作图和解直角三角形是解决问题的关键.

练习册系列答案
相关题目
8.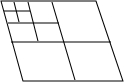 如图,将一个菱形的纸片剪成4个完全相同的小菱形,共得到4个菱形,再将其中1个小菱形剪成4个完全相同的更小的菱形,共得到7个菱形,…,按照此规律,依次操作减剪下去,则第n次剪,会得到菱形的个数为( )
如图,将一个菱形的纸片剪成4个完全相同的小菱形,共得到4个菱形,再将其中1个小菱形剪成4个完全相同的更小的菱形,共得到7个菱形,…,按照此规律,依次操作减剪下去,则第n次剪,会得到菱形的个数为( )
 如图,将一个菱形的纸片剪成4个完全相同的小菱形,共得到4个菱形,再将其中1个小菱形剪成4个完全相同的更小的菱形,共得到7个菱形,…,按照此规律,依次操作减剪下去,则第n次剪,会得到菱形的个数为( )
如图,将一个菱形的纸片剪成4个完全相同的小菱形,共得到4个菱形,再将其中1个小菱形剪成4个完全相同的更小的菱形,共得到7个菱形,…,按照此规律,依次操作减剪下去,则第n次剪,会得到菱形的个数为( )| A. | 2n个 | B. | (2n+1)个 | C. | 3n个 | D. | (3n+1)个 |
2.不等式组$\left\{\begin{array}{l}{3-x≤5}\\{\frac{1}{2}(x+1)<1}\end{array}\right.$的解集在数轴上可表示为( )
| A. | 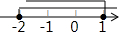 | B. | 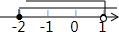 | C. |  | D. |  |
6.下列计算正确的是( )
| A. | a10-a7=a3 | B. | (-2a2b)2=-2a4b2 | C. | $\sqrt{2}+\sqrt{3}=\sqrt{5}$ | D. | (a+b)9÷(a+b)3=(a+b)6 |
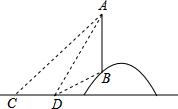 如图,一电线杆AB立在山坡上,从地面的点C看,测得杆顶端点A的仰角为45°向前走6m到达点D,又测得杆顶端点A和杆底端点B的仰角分别是60°和30°.
如图,一电线杆AB立在山坡上,从地面的点C看,测得杆顶端点A的仰角为45°向前走6m到达点D,又测得杆顶端点A和杆底端点B的仰角分别是60°和30°. 在平面直角坐标系xOy中,抛物线y=mx2-2mx+m-1(m>0)与x轴的交点为A,B.
在平面直角坐标系xOy中,抛物线y=mx2-2mx+m-1(m>0)与x轴的交点为A,B.