题目内容
4.阅读材料:对于任意两个数a、b的大小比较,有下面的方法:
当a-b>0时,一定有a>b;
当a-b=0时,一定有a=b;
当a-b<0时,一定有a<b.
反过来也成立.因此,我们把这种比较两个数大小的方法叫做“求差法”.
问题解决:
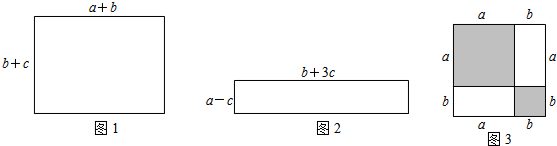
(1)图1长方形的周长M=2a+4b+2c;图2长方形的周长N=2a+2b+4c;用“求差法”比较M、N的大小(b>c).
(2)如图3,把边长为a+b(a≠b)的大正方形分割成两个边长分别是a、b的小正方形及两个长方形,试比较两个小正方形面积之和A与两个长方形面积之和B的大小.
分析 (1)根据长方形的周长公式进行计算,再利用“求差法”比较M、N的大小即可;
(2)根据正方形的面积公式进行计算,再利用“求差法”比较M、N的大小即可.
解答 解:(1)图1长方形的周长M=2(a+b+b+c)=2a+4b+2c,
图2长方形的周长N=2(a-c+b+3c)=2a+2b+4c,
M-N=(2a+4b+2c)-(2a+2b+4c)=2b-2c,
∵b>c,∴2b>2c,
∴2b-2c>0,
∴M>N,
故答案为2a+4b+2c,2a+2b+4c,
(2)两个小正方形面积之和A=a2+b2,
两个长方形面积之和B=2ab,
a2+b2-2ab=(a-b)2,
∵a≠b,
∴a-b≠0,
∴A>B.
点评 本题考查了整式的混合运算,长方形的周长和面积以及正方形的周长和面积是解题的关键.

练习册系列答案
 互动英语系列答案
互动英语系列答案
相关题目
18.已知n是一个正整数,若$\sqrt{135n}$与$\sqrt{3}$能合并,则n的最小值是( )
| A. | 3 | B. | 5 | C. | 15 | D. | 25 |
9.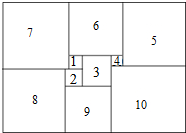 如图所示,1925年数学家莫伦发现了世界上第一个完美长方形,它恰能被分割成10个大小不同的正方形.如果图中标注的①、②正方形边长分别是x、y,那么第⑩个正方形的边长是( )
如图所示,1925年数学家莫伦发现了世界上第一个完美长方形,它恰能被分割成10个大小不同的正方形.如果图中标注的①、②正方形边长分别是x、y,那么第⑩个正方形的边长是( )
 如图所示,1925年数学家莫伦发现了世界上第一个完美长方形,它恰能被分割成10个大小不同的正方形.如果图中标注的①、②正方形边长分别是x、y,那么第⑩个正方形的边长是( )
如图所示,1925年数学家莫伦发现了世界上第一个完美长方形,它恰能被分割成10个大小不同的正方形.如果图中标注的①、②正方形边长分别是x、y,那么第⑩个正方形的边长是( )| A. | x+2y | B. | 4y-x | C. | 7y-4y | D. | 10y-7x |
16.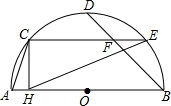 如图,AB是半圆O的直径,C、D、E是半圆的四等分点,CH⊥AB于H,连接BD、
如图,AB是半圆O的直径,C、D、E是半圆的四等分点,CH⊥AB于H,连接BD、
EC相交于F点,连接AC、EH,下列结论:
①CE=2CH;②∠ACH=∠CEH;③∠CFD=2∠ACH,
其中正确的结论是( )
 如图,AB是半圆O的直径,C、D、E是半圆的四等分点,CH⊥AB于H,连接BD、
如图,AB是半圆O的直径,C、D、E是半圆的四等分点,CH⊥AB于H,连接BD、EC相交于F点,连接AC、EH,下列结论:
①CE=2CH;②∠ACH=∠CEH;③∠CFD=2∠ACH,
其中正确的结论是( )
| A. | ①②③ | B. | 只有①② | C. | 只有①③ | D. | 只有③ |
13.若ab=cd,且abcd≠0,则下列式子正确的是( )
| A. | a:c=b:d | B. | d:c=b:a | C. | a:b=c:d | D. | a:d=c:b |