题目内容
7.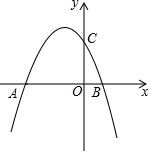 如图,已知抛物线y=-$\frac{1}{3}$x2+bx+6与x轴交于点A(-6,0)和点B,与y轴交于点C.
如图,已知抛物线y=-$\frac{1}{3}$x2+bx+6与x轴交于点A(-6,0)和点B,与y轴交于点C.(1)求该抛物线的解析式;
(2)写出顶点的坐标,并求AB的长;
(3)若点A,O,C均在⊙D上,请写出点D的坐标,连接BC,并判断直线BC与⊙D的位置关系.
分析 (1)根据待定系数法,可得答案;
(2)根据配方法,可得顶点坐标;根据自变量与函数值的对应关系,可得B点坐标,根据两点间的距离,可得答案;
(3)根据直角三角形的斜边大于直角边,可得r与d的关系,根据d<r,可得答案.
解答 解:(1)将A点坐标代入函数解析式,得
-$\frac{1}{3}$×(-6)-6b+6=0,
解得b=-1,
该抛物线的解析式为y=-$\frac{1}{3}$x2-x+6;
(2)y=-$\frac{1}{3}$x2-x+6配方,得
y=-$\frac{1}{3}$(x+$\frac{3}{2}$)2+$\frac{27}{4}$,
顶点坐标为(-$\frac{3}{2}$,$\frac{27}{4}$);
当y=0时,-$\frac{1}{3}$x2-x+6=0,
解得x=-6,x=3,
即A(-6,0)B(3,0),
AB的长3-(-6)=9;
AB的长为9;
(3)点D在AO的中垂线上,CO的中垂线上,
D点的横坐标为$\frac{-6}{2}$=-3,D的纵坐标为$\frac{6}{2}$=3,
D点的坐标为(-3,3);
作DE⊥BC于E如图 ,
,
DC>DE,
d>r,
直线BC与⊙D相交.
点评 本题考查了二次函数综合题,解(1)的关键是待定系数法;解(2)的关键是配方法,解(3)的关键是利用直角三角形的斜边大于直角边得出d>r.

练习册系列答案
相关题目
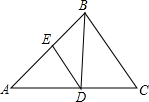 如图,△ABC中,∠A=36°,∠C=60°,BD平分∠ABC,DE∥BC交AB于E,
如图,△ABC中,∠A=36°,∠C=60°,BD平分∠ABC,DE∥BC交AB于E,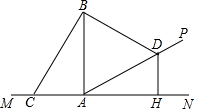 如图,在坡AP的坡脚A处竖有一根电线杆AB,为固定电线杆在地面C处和坡面D处各装一根等长的引拉线BC和BD,过点D作地面MN的垂线DH,H为垂足,已知点C、A、H在一直线上,若测得AC=5米,AD=13米,坡角为30°,试求电线杆AB的高度.
如图,在坡AP的坡脚A处竖有一根电线杆AB,为固定电线杆在地面C处和坡面D处各装一根等长的引拉线BC和BD,过点D作地面MN的垂线DH,H为垂足,已知点C、A、H在一直线上,若测得AC=5米,AD=13米,坡角为30°,试求电线杆AB的高度. 如图,在平行四边形ABCD中,E为BC边上的一点,且AE与DE分别平分∠BAD和∠ADC
如图,在平行四边形ABCD中,E为BC边上的一点,且AE与DE分别平分∠BAD和∠ADC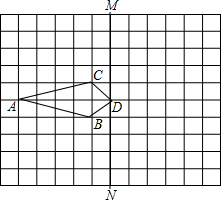 如图,四边形ABDC的四个顶点都在正方形网格中的小正方形顶点上,每个小正方形的边长为1.
如图,四边形ABDC的四个顶点都在正方形网格中的小正方形顶点上,每个小正方形的边长为1.