题目内容
18.一口袋中装有四根长度分别为1cm,3cm,4cm和5cm的细木棒,小明手中有一根长度为3cm的细木棒,现随机从袋内取出两根细木棒与小明手中的细木棒放在一起,回答下列问题:(1)求这三根细木棒能构成三角形的概率;
(2)求这三根细木棒能构成直角三角形的概率;
(3)求这三根细木棒能构成等腰三角形的概率.(提醒:列出所有的抽取方式)
分析 (1)首先用列举法列举所有情况,再根据三角形的三边关系判断能否构成三角形,
(2)由(1)可知所有可能情况,再找到在构成直角三角形三角形的情况数即可求出其概率;
(3)由(1)可知所有可能情况,再找等腰三角形的情况有几种即可分别求出概率.
解答 解:(1)列表得:
| 第1根长度 | 第2根长度 |
| 1 | 3 |
| 1 | 4 |
| 1 | 5 |
| 3 | 4 |
| 3 | 5 |
| 4 | 5 |
(2)由(1)可知P(能构成直角三角形)=$\frac{1}{6}$;
(3)由(1可知)P(能构成等腰三角形)=$\frac{3}{6}$=$\frac{1}{2}$.
点评 本题考查了用列表法或树状图法求概率.此题涉及的内容较广,涉及到三角形的三边关系、等腰三角形及直角三角形的性质,需同学们仔细分析解答.用到的知识点为:概率=所求情况数与总情况数之比.

练习册系列答案
相关题目
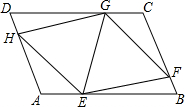 如图,在平行四边形ABCD中,点E、F、G、H分别在边AB、BC、CD、DA上,AE=CG,AH=CF,且EG平分∠HEF.
如图,在平行四边形ABCD中,点E、F、G、H分别在边AB、BC、CD、DA上,AE=CG,AH=CF,且EG平分∠HEF.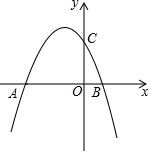 如图,已知抛物线y=-$\frac{1}{3}$x2+bx+6与x轴交于点A(-6,0)和点B,与y轴交于点C.
如图,已知抛物线y=-$\frac{1}{3}$x2+bx+6与x轴交于点A(-6,0)和点B,与y轴交于点C. 平行四边形ABCD中,过点D作DE⊥AB于点E,点F在CD上,CF=AE,连接BF,AF.
平行四边形ABCD中,过点D作DE⊥AB于点E,点F在CD上,CF=AE,连接BF,AF.