题目内容
15.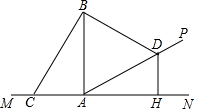 如图,在坡AP的坡脚A处竖有一根电线杆AB,为固定电线杆在地面C处和坡面D处各装一根等长的引拉线BC和BD,过点D作地面MN的垂线DH,H为垂足,已知点C、A、H在一直线上,若测得AC=5米,AD=13米,坡角为30°,试求电线杆AB的高度.
如图,在坡AP的坡脚A处竖有一根电线杆AB,为固定电线杆在地面C处和坡面D处各装一根等长的引拉线BC和BD,过点D作地面MN的垂线DH,H为垂足,已知点C、A、H在一直线上,若测得AC=5米,AD=13米,坡角为30°,试求电线杆AB的高度.
分析 作BE⊥AD于点E,设AB=x米,在直角△ABE中,根据三角函数,利用x表示出AE和BE的长,则在直角△BED中,利用勾股定理表示出BD的长,在直角△ABC中利用勾股定理表示出BC,根据BC=BD即可列方程求解.
解答  解:作BE⊥AD于点E,设AB=x米,
解:作BE⊥AD于点E,设AB=x米,
在直角△ABE中,∠BAE=90°-∠DAH=90°-30°=60°,
则AE=AB•cos∠BAE=xcos60°=$\frac{1}{2}$x(米),
BE=AB•sin∠BAE=xsin60°=$\frac{\sqrt{3}}{2}$x(米).
则DE=AD-AE=13-$\frac{1}{2}$x,
在直角△BED中,BD2=BE2+DE2=($\frac{\sqrt{3}}{2}$x)2+(13-$\frac{1}{2}$x)2=169+x2-13x,
在直角△ABC中,BC2=AC2+AB2=52+x2=25+x2.
∵BC=BD,
∴169+x2-13x=25+x2.
解得x=$\frac{144}{13}$.
答:电线杆AB的高度是$\frac{144}{13}$米.
点评 本题考查了解直角三角形的应用,坡度坡角问题,正确作出辅助线,利用AB的长表示出BD和BC是关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
3.在同一平面内有直线a1,a2,a3,a4,…,a100,若a1⊥a2,a2∥a3,a3⊥a4,a4∥a5,…,按此规律进行下去,则a1与a100的位置关系是( )
| A. | 平行 | B. | 相交 | C. | 重合 | D. | 无法判断 |
20.甲、乙两位同学做抛骰子(均匀正方体形状)实验,他们共抛了60次,出现向上点数的次数如表:
(1)计算出现向上点数为6的频率.
(2)丙说:“如果抛600次,那么出现向上点数为6的次数一定是100次.”请直接判断丙的说法是否正确.
(3)如果甲乙两同学各抛一枚骰子,求出现向上点数之和不超过7的概率.
| 向上点数 | 1 | 2 | 3 | 4 | 5 | 6 |
| 出现次数 | 8 | 10 | 7 | 9 | 16 | 10 |
(2)丙说:“如果抛600次,那么出现向上点数为6的次数一定是100次.”请直接判断丙的说法是否正确.
(3)如果甲乙两同学各抛一枚骰子,求出现向上点数之和不超过7的概率.
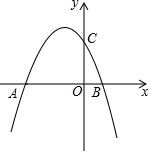 如图,已知抛物线y=-$\frac{1}{3}$x2+bx+6与x轴交于点A(-6,0)和点B,与y轴交于点C.
如图,已知抛物线y=-$\frac{1}{3}$x2+bx+6与x轴交于点A(-6,0)和点B,与y轴交于点C.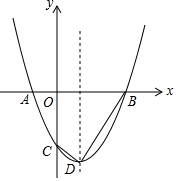 如图,O是坐标原点,过点A(-1,0)的抛物线y=x2-bx-3与x轴的另一个交点为B,与y轴交于点C,其顶点为D点
如图,O是坐标原点,过点A(-1,0)的抛物线y=x2-bx-3与x轴的另一个交点为B,与y轴交于点C,其顶点为D点