题目内容
19. 如图,在平行四边形ABCD中,E为BC边上的一点,且AE与DE分别平分∠BAD和∠ADC
如图,在平行四边形ABCD中,E为BC边上的一点,且AE与DE分别平分∠BAD和∠ADC(1)求证:AE⊥DE;
(2)设以AD为直径的半圆交AB于F,连结DF交AE于G,已知CD=5,AE=8.
①求BC的长;
②求$\frac{FG}{AF}$值.
分析 (1)由∠BAD+∠ADC=180°.又因为AE、DE平分∠BAD、∠ADC,推出∠DAE+∠ADE=90°,即可推出∠AED=90°,由此即可解决问题.
(2)①只要证明BA=BW,CD=CE即可解决问题.②由tan∠FAG=$\frac{FG}{AF}$,可得$\frac{FG}{AF}$=tan∠DAE=$\frac{DE}{AE}$,求出DE即可解决问题.
解答 (1)证明:在平行四边形ABCD中,∵AB∥CD,
∴∠BAD+∠ADC=180°.
又∵AE、DE平分∠BAD、∠ADC,
∴∠DAE+∠ADE=90°,
∴∠AED=90°,
∴AE⊥DE.
(2)解:①在平行四边形ABCD中,∵AD∥BC,AB=CD=5,AD=BC,
∴∠DAE=∠BEA,
又∵AE平分∠BAD,即∠DAE=∠BAE,
∴∠BEA=∠BAE,
∴BE=AB=5,
同理EC=CD=5,
∴BC=BE+EC=10,
②∵AD=BC=10,AE=8,
在Rt△AED中,DE=$\sqrt{A{D}^{2}-A{E}^{2}}$=$\sqrt{1{0}^{2}-{8}^{2}}$=6,
又∵AE是∠BAD的角平分线,
∴∠FAG=∠DAE,
∵AD是直径,
∴∠AFD=90°,
∴tan∠FAG=$\frac{FG}{AF}$,
∴$\frac{FG}{AF}$=tan∠DAE=$\frac{DE}{AE}$=$\frac{6}{8}$=$\frac{3}{4}$.
点评 本题考查圆综合题、平行四边形的性质、勾股定理、角平分线的定义等知识,解题的关键是灵活运用所学知识解决问题,属于中考常考题型.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
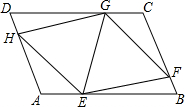 如图,在平行四边形ABCD中,点E、F、G、H分别在边AB、BC、CD、DA上,AE=CG,AH=CF,且EG平分∠HEF.
如图,在平行四边形ABCD中,点E、F、G、H分别在边AB、BC、CD、DA上,AE=CG,AH=CF,且EG平分∠HEF.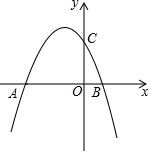 如图,已知抛物线y=-$\frac{1}{3}$x2+bx+6与x轴交于点A(-6,0)和点B,与y轴交于点C.
如图,已知抛物线y=-$\frac{1}{3}$x2+bx+6与x轴交于点A(-6,0)和点B,与y轴交于点C.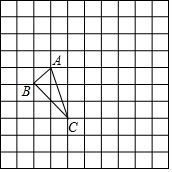 如图,正方形网格中每个小正方形边长都是1,每个小格的顶点叫格点,以格点为顶点的三角形叫做格点三角形.
如图,正方形网格中每个小正方形边长都是1,每个小格的顶点叫格点,以格点为顶点的三角形叫做格点三角形.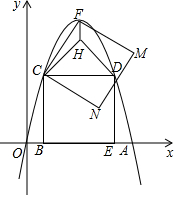 如图,在平面直角坐标系中,抛物线y=ax2-6ax(a<0)与x轴正半轴交于点A,矩形BCDE的顶点B、E均在x轴上,C、D均在抛物线上,且点B的坐标为(1,0),抛物线的顶点为F,以CF为边作正方形CFMN,以CD为底边向上作等腰直角三角形CDH,连结FH.
如图,在平面直角坐标系中,抛物线y=ax2-6ax(a<0)与x轴正半轴交于点A,矩形BCDE的顶点B、E均在x轴上,C、D均在抛物线上,且点B的坐标为(1,0),抛物线的顶点为F,以CF为边作正方形CFMN,以CD为底边向上作等腰直角三角形CDH,连结FH. 平行四边形ABCD中,过点D作DE⊥AB于点E,点F在CD上,CF=AE,连接BF,AF.
平行四边形ABCD中,过点D作DE⊥AB于点E,点F在CD上,CF=AE,连接BF,AF. 如图,三角形ABC中,∠B=90°,D在AC边上,DF⊥BC于F,DE⊥AB于E,说明:AE∥DF,BC∥DE.
如图,三角形ABC中,∠B=90°,D在AC边上,DF⊥BC于F,DE⊥AB于E,说明:AE∥DF,BC∥DE.