题目内容
12．$\left\{\begin{array}{l}{4x-3＜3（2x+1）}\\{\frac{3x}{2}-1＞5-\frac{1}{2}x}\end{array}\right.$．分析 分别求出各不等式的解集，再求出其公共解集即可．
解答 解：$\left\{\begin{array}{l}{4x-3＜3（2x+1）①}\\{\frac{3x}{2}-1＞5-\frac{1}{2}x②}\end{array}\right.$，由①得，x＞-3，由②得，x＞3，
故不等式组的解集为：x＞3．
点评 本题考查的是解一元一次不等式组，熟知“同大取大；同小取小；大小小大中间找；大大小小找不到”的原则是解答此题的关键．
练习册系列答案
相关题目
如图，AB∥CD，则∠1的度数为85°．
3．在同一平面内有直线a1，a2，a3，a4，…，a100，若a1⊥a2，a2∥a3，a3⊥a4，a4∥a5，…，按此规律进行下去，则a1与a100的位置关系是（ ）
| A． | 平行 | B． | 相交 | C． | 重合 | D． | 无法判断 |
20．甲、乙两位同学做抛骰子（均匀正方体形状）实验，他们共抛了60次，出现向上点数的次数如表：
（1）计算出现向上点数为6的频率．
（2）丙说：“如果抛600次，那么出现向上点数为6的次数一定是100次．”请直接判断丙的说法是否正确．
（3）如果甲乙两同学各抛一枚骰子，求出现向上点数之和不超过7的概率．
| 向上点数 | 1 | 2 | 3 | 4 | 5 | 6 |
| 出现次数 | 8 | 10 | 7 | 9 | 16 | 10 |
（2）丙说：“如果抛600次，那么出现向上点数为6的次数一定是100次．”请直接判断丙的说法是否正确．
（3）如果甲乙两同学各抛一枚骰子，求出现向上点数之和不超过7的概率．
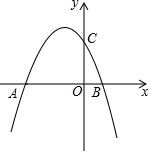如图，已知抛物线y=-$\frac{1}{3}$x2+bx+6与x轴交于点A（-6，0）和点B，与y轴交于点C．