题目内容
3.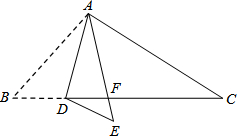 如图,在△ABC中,点D是BC边上的一点,∠B=50°,∠BAD=30°,将△ABD沿AD折叠得到△AED,AE与BC交于点F.
如图,在△ABC中,点D是BC边上的一点,∠B=50°,∠BAD=30°,将△ABD沿AD折叠得到△AED,AE与BC交于点F.(1)求∠AFC的度数;
(2)求∠EDF的度数.
分析 (1)根据折叠求出∠BAD=∠DAF,根据三角形外角性质求出即可;
(2)根据三角形内角和定理求出∠ADB,求出∠ADE,根据三角形外角性质求出∠ADF,即可求出答案.
解答 解:(1)∵△ABD沿AD折叠得到△AED,
∴∠BAD=∠DAF,
∵∠B=50°,∠BAD=30°,
∴∠AFC=∠B+∠BAD+∠DAF=110°;
(2)∵∠B=50°,∠BAD=30°,
∴∠ADB=180°-50°-30°=100°,
∠ADC=50°+30°=80°,
∵△ABD沿AD折叠得到△AED,
∴∠ADE=∠ADB=100°,
∴∠EDF=∠ADE-∠ADC
=100°-80°=20°.
点评 本题考查了三角形内角和定理,三角形外角性质和折叠的性质等知识点,能根据定理求出各个角的度数是解此题的关键.

练习册系列答案
 新课标阶梯阅读训练系列答案
新课标阶梯阅读训练系列答案
相关题目
14.如表是某皮鞋专卖店一周的同一款男士皮鞋四种尺码的销售分布情况:
对于不同的a,下列关于皮鞋尺码的四个统计量①众数,②中位数,③平均数,④方差中,不会发生改变的是( )
| 尺码/码 | 38 | 39 | 40 | 41 |
| 频数 | 5 | 15 | a | 10-a |
| A. | ①② | B. | ②③ | C. | ③④ | D. | ①④ |
11. 在三角形的边上找出一点,使得该点与三角形的两顶点构成等腰三角形,这样的点有( )个.
在三角形的边上找出一点,使得该点与三角形的两顶点构成等腰三角形,这样的点有( )个.
 在三角形的边上找出一点,使得该点与三角形的两顶点构成等腰三角形,这样的点有( )个.
在三角形的边上找出一点,使得该点与三角形的两顶点构成等腰三角形,这样的点有( )个.| A. | 4 | B. | 5 | C. | 6 | D. | 7 |
8.已知n是自然数,且$\frac{20n+17}{13n+4}$能约分,则n最小是( )
| A. | 3 | B. | 2 | C. | 1 | D. | 非上述答案 |
 如图,在△ABC中∠C=90°,AC=BC,AD平分∠CAB,交BC于点D,DE⊥BE.
如图,在△ABC中∠C=90°,AC=BC,AD平分∠CAB,交BC于点D,DE⊥BE.