题目内容
15. 如图,在△ABC中∠C=90°,AC=BC,AD平分∠CAB,交BC于点D,DE⊥BE.
如图,在△ABC中∠C=90°,AC=BC,AD平分∠CAB,交BC于点D,DE⊥BE.(1)求证:AC=DE+BD;
(2)若AB=6cm,则△DBE的周长为6cm.
分析 (1)根据角平分线的性质得到DE﹦DC,等量代换即可得到结论;
(2)根据全等三角形的性质得到AE=AC,根据等腰直角三角形的性质得到BE=DE,等量代换即可得到结论.
解答 (1)证明:∵∠C﹦90° ,
,
∴AC⊥DC,
又DE⊥AB,AD平分∠CAB,
∴DE﹦DC,
又∵BC﹦DC+BD,AC﹦BC,
∴AC﹦DE+BD;
(2)解:∵BC=AC=DE+BD,
在Rt△ACD与Rt△AED中,$\left\{\begin{array}{l}{CD=DE}\\{AD=AD}\end{array}\right.$,
∴Rt△ACD≌Rt△AED,
∴AE=AC,
∵DE⊥AB,∠B=45°,
∴BE=DE,
∴△DBE的周长=BD+DE+BE=AE+BE=AB=6cm.
故答案为:6cm.
点评 本题考查了全等三角形的判定与性质,等腰直角三角形的性质,角平分线的性质,熟练正确全等三角形的判定与性质是解题的关键.

练习册系列答案
 全优冲刺100分系列答案
全优冲刺100分系列答案 英才点津系列答案
英才点津系列答案
相关题目
6.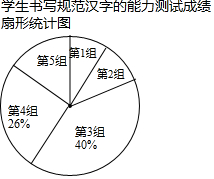 某校为了调查学生书写汉字的能力,从七年级1000名学生中随机抽选了部分学生参加测试,并根据测试成绩绘制出如下频数分布表和扇形统计图:
某校为了调查学生书写汉字的能力,从七年级1000名学生中随机抽选了部分学生参加测试,并根据测试成绩绘制出如下频数分布表和扇形统计图:
请结合图表完成下列各题:
(1)直接填空:表中a的值为3,b的值为13;扇形统计图中表示第一小组所对应的圆心角度数为28.8°;
(2)若测试成绩不低于80分为优秀,请你估计该校七年级规范字书写优秀的人数?
(3)第一组中的A、B、C、D四名同学为提高汉字书写能力,分成两组,每组两人进行对抗练习,请用列表法或画树状图的方法,求A与B同学能分在同一组的概率.
 某校为了调查学生书写汉字的能力,从七年级1000名学生中随机抽选了部分学生参加测试,并根据测试成绩绘制出如下频数分布表和扇形统计图:
某校为了调查学生书写汉字的能力,从七年级1000名学生中随机抽选了部分学生参加测试,并根据测试成绩绘制出如下频数分布表和扇形统计图:| 组别 | 成绩x分 | 频数(人数) |
| 第1组 | x<60 | 4 |
| 第2组 | 60≤x<70 | a |
| 第3组 | 70≤x<80 | 20 |
| 第4组 | 80≤x<90 | b |
| 第5组 | 90≤x≤100 | 10 |
(1)直接填空:表中a的值为3,b的值为13;扇形统计图中表示第一小组所对应的圆心角度数为28.8°;
(2)若测试成绩不低于80分为优秀,请你估计该校七年级规范字书写优秀的人数?
(3)第一组中的A、B、C、D四名同学为提高汉字书写能力,分成两组,每组两人进行对抗练习,请用列表法或画树状图的方法,求A与B同学能分在同一组的概率.
6.下列各组数据中,结果相等的是( )
| A. | (-1)4与-14 | B. | -|-3|与-(-3) | C. | -(-1)2015与(-1)2016 | D. | -(-3)与+(-3) |
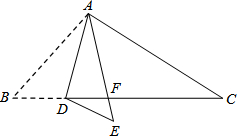 如图,在△ABC中,点D是BC边上的一点,∠B=50°,∠BAD=30°,将△ABD沿AD折叠得到△AED,AE与BC交于点F.
如图,在△ABC中,点D是BC边上的一点,∠B=50°,∠BAD=30°,将△ABD沿AD折叠得到△AED,AE与BC交于点F.