题目内容
8.已知n是自然数,且$\frac{20n+17}{13n+4}$能约分,则n最小是( )| A. | 3 | B. | 2 | C. | 1 | D. | 非上述答案 |
分析 根据各个选项中的数据代入原来的式子看哪个式子可以约分即可解答本题.
解答 解:∵$\frac{20n+17}{13n+4}$=$\frac{13n+4+7n+13}{13n+4}$=$1+\frac{7n+13}{13n+4}$,
∴当n=0时,1+$\frac{7×0+13}{13×0+4}=\frac{17}{4}$+1=$\frac{21}{4}$,
当n=1时,$1+\frac{7×1+13}{13×1+4}=\frac{37}{17}$,故选项C错误,
当n=2时,$1+\frac{7×2+13}{13×2+4}=\frac{57}{30}$=$\frac{19}{10}$,故选项B正确,
当n=3时,1+$\frac{7×3+13}{13×3+4}=\frac{77}{43}$,故选项A错误,
故选B.
点评 本题考查约分,解答本题的关键是明确约分的方法.

练习册系列答案
 黄冈天天练口算题卡系列答案
黄冈天天练口算题卡系列答案
相关题目
19.将图1中的菱形剪开得到图2,则图2中共有4个菱形;将图2中的一个菱形剪开得到图3,则图3中共有7个菱形,…如此剪下去,请结合图形解决问题 
(1)按图示规律填写下表:
(2)按照这种方式剪下去,则第n个图中共有(3n-2)个菱形.
(3)按照这种方式剪下去,则第2017个图中共有6049个菱形.

(1)按图示规律填写下表:
| 图 | 1 | 2 | 3 | 4 | 5 | … |
| 菱形个数 | 1 | 4 | 7 | 10 | 13 | … |
(3)按照这种方式剪下去,则第2017个图中共有6049个菱形.
13.关于x的一元二次方程(m-3)x2+2x-1=0有实数根,则m的取值范围是( )
| A. | m≥2 | B. | m>2 | C. | m≥2且m≠3 | D. | m>2且m≠3 |
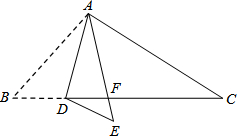 如图,在△ABC中,点D是BC边上的一点,∠B=50°,∠BAD=30°,将△ABD沿AD折叠得到△AED,AE与BC交于点F.
如图,在△ABC中,点D是BC边上的一点,∠B=50°,∠BAD=30°,将△ABD沿AD折叠得到△AED,AE与BC交于点F.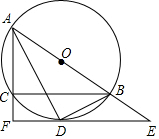 如图,⊙O是△ABC的外接圆,AB为直径,∠BAC的平分线交⊙O于点D,过点D的切线分别交AB,AC的延长线于E,F,连接BD.
如图,⊙O是△ABC的外接圆,AB为直径,∠BAC的平分线交⊙O于点D,过点D的切线分别交AB,AC的延长线于E,F,连接BD.