题目内容
13.先化简,再求值:$\frac{{x}^{2}+2x+1}{{x}^{3}-x}$÷(1+$\frac{1}{x}$),其中x=$\sqrt{3}$+1.分析 根据分式的运算法则即可求出答案.
解答 解:原式=$\frac{(x+1)^{2}}{x(x+1)(x-1)}$•$\frac{x}{x+1}$
=$\frac{1}{x-1}$
当x=$\sqrt{3}$+1时,
原式=$\frac{1}{\sqrt{3}+1-1}$
=$\frac{\sqrt{3}}{3}$
点评 本题考查分式的运算,解题的关键是熟练运用分式的运算法则,本题属于基础题型.

练习册系列答案
相关题目
1.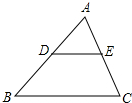 如图,在△ABC中,点D、E分别为AB、AC的中点,则△ADE与四边形BCED的面积比为( )
如图,在△ABC中,点D、E分别为AB、AC的中点,则△ADE与四边形BCED的面积比为( )
 如图,在△ABC中,点D、E分别为AB、AC的中点,则△ADE与四边形BCED的面积比为( )
如图,在△ABC中,点D、E分别为AB、AC的中点,则△ADE与四边形BCED的面积比为( )| A. | 1:1 | B. | 1:2 | C. | 1:3 | D. | 1:4 |
18.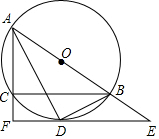 如图,⊙O是△ABC的外接圆,AB为直径,∠BAC的平分线交⊙O于点D,过点D的切线分别交AB,AC的延长线于E,F,连接BD.
如图,⊙O是△ABC的外接圆,AB为直径,∠BAC的平分线交⊙O于点D,过点D的切线分别交AB,AC的延长线于E,F,连接BD.
(1)求证:AF⊥EF;
(2)若AC=6,CF=2,求⊙O的半径.
 如图,⊙O是△ABC的外接圆,AB为直径,∠BAC的平分线交⊙O于点D,过点D的切线分别交AB,AC的延长线于E,F,连接BD.
如图,⊙O是△ABC的外接圆,AB为直径,∠BAC的平分线交⊙O于点D,过点D的切线分别交AB,AC的延长线于E,F,连接BD.(1)求证:AF⊥EF;
(2)若AC=6,CF=2,求⊙O的半径.
6.下列各组数据中,结果相等的是( )
| A. | (-1)4与-14 | B. | -|-3|与-(-3) | C. | -(-1)2015与(-1)2016 | D. | -(-3)与+(-3) |
3.如果等式x6÷xm=x2,那么m=( )
| A. | 2 | B. | 3 | C. | 4 | D. | 5 |
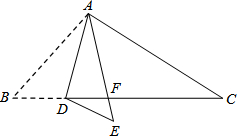 如图,在△ABC中,点D是BC边上的一点,∠B=50°,∠BAD=30°,将△ABD沿AD折叠得到△AED,AE与BC交于点F.
如图,在△ABC中,点D是BC边上的一点,∠B=50°,∠BAD=30°,将△ABD沿AD折叠得到△AED,AE与BC交于点F. 如图AB与CD平行,∠1=45°,∠D=45°,
如图AB与CD平行,∠1=45°,∠D=45°,