题目内容
8.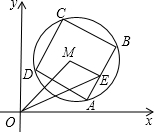 如图,已知M(3,3),⊙M的半径为2,四边形ABCD是⊙M的内接正方形,E为AB中点,当正方形ABCD绕圆心M转动时,△OME的面积最大值为3.
如图,已知M(3,3),⊙M的半径为2,四边形ABCD是⊙M的内接正方形,E为AB中点,当正方形ABCD绕圆心M转动时,△OME的面积最大值为3.
分析 因为OM,ME是定值,所以当EM⊥OM时,△OME的面积最大,求出OM、EM即可解决问题.
解答 解:∵OM,ME是定值,
∴当ME ⊥OM时,△OME的面积最大,
⊥OM时,△OME的面积最大,
∵M(3,3),
∴OM=3$\sqrt{2}$,
∵⊙M的半径为2,
∴正方形ABCD的边长为2$\sqrt{2}$,
∴ME=$\sqrt{2}$,
∴△OME的面积的最大值=$\frac{1}{2}$•OM•ME=$\frac{1}{2}$$•3\sqrt{2}$$•\sqrt{2}$=3.
故答案为3
点评 本题考查正多边形与圆、坐标与图形的性质等知识,解题的关键是灵活运用所学知识解决问题,属于中考常考题型.

练习册系列答案
相关题目
19.若点A(a,-2)、B(4,b)在正比例函数y=kx的图象上,则下列等式一定成立的是( )
| A. | a-b=6 | B. | a+b=-10 | C. | a•b=-8 | D. | $\frac{a}{b}$=-2 |
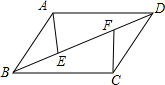 如图所示,已知点E,F在?ABCD的对角线BD上,且BF=DE,求证:AE=CF.
如图所示,已知点E,F在?ABCD的对角线BD上,且BF=DE,求证:AE=CF.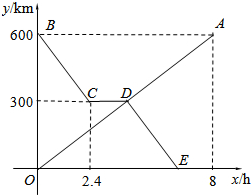 货车和轿车分别从甲、乙两地同时出发,沿同一公路相向而行.轿车出发3h后休息,直至与货车相遇后,以原速度继续行驶.设货车出发xh后,货车、轿车分别到达离甲地y1km和y2km的地方,图中的线段OA、折线BCDE分别表示y1、y2与x之间的函数关系.
货车和轿车分别从甲、乙两地同时出发,沿同一公路相向而行.轿车出发3h后休息,直至与货车相遇后,以原速度继续行驶.设货车出发xh后,货车、轿车分别到达离甲地y1km和y2km的地方,图中的线段OA、折线BCDE分别表示y1、y2与x之间的函数关系.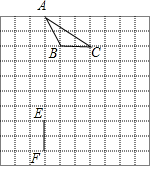 如图,在8×8的正方形网格中,△ABC的顶点和线段EF的端点都在边长为1的小正方形的格点上.请你在图中找出一点D(仅一个点即可),连结DE,DF,使△DEF与△ABC全等,并给予证明.
如图,在8×8的正方形网格中,△ABC的顶点和线段EF的端点都在边长为1的小正方形的格点上.请你在图中找出一点D(仅一个点即可),连结DE,DF,使△DEF与△ABC全等,并给予证明.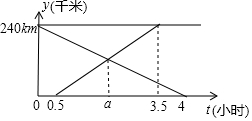 甲、乙两车分别从A、B两地相向而行,甲车出发0.5小时后乙车出发,并以各自速度匀速行驶,两车相遇后依然按照原速度原方向各自行驶,如图所示是两车离B地距离y与甲车出发时间t(小时)之间的函数图象.
甲、乙两车分别从A、B两地相向而行,甲车出发0.5小时后乙车出发,并以各自速度匀速行驶,两车相遇后依然按照原速度原方向各自行驶,如图所示是两车离B地距离y与甲车出发时间t(小时)之间的函数图象.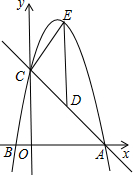 如图,抛物线y=-x2+bx+c与x轴交于A、B两点,与y轴交于点C,点A(5,0),B(-1,0),点D在直线AC上,过点D作DE∥y轴交抛物线于点E,设点D的横坐标为m.
如图,抛物线y=-x2+bx+c与x轴交于A、B两点,与y轴交于点C,点A(5,0),B(-1,0),点D在直线AC上,过点D作DE∥y轴交抛物线于点E,设点D的横坐标为m.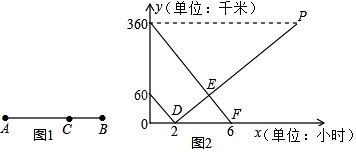
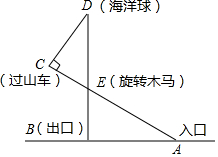 某游乐场部分平面图如图所示,C、E、A在同一直线上,D、E、B在同一直线上,测得A处与E处的距离为80 米,C处与D处的距离为34米,∠C=90°,∠ABE=90°,∠BAE=30°.($\sqrt{2}$≈1.4,$\sqrt{3}$≈1.7)
某游乐场部分平面图如图所示,C、E、A在同一直线上,D、E、B在同一直线上,测得A处与E处的距离为80 米,C处与D处的距离为34米,∠C=90°,∠ABE=90°,∠BAE=30°.($\sqrt{2}$≈1.4,$\sqrt{3}$≈1.7)