题目内容
13.若二次函数y=ax2+1的图象经过点(-2,0),则关于x的方程a(x-2)2+1=0的实数根为( )| A. | x1=0,x2=4 | B. | x1=-2,x2=6 | C. | x1=$\frac{3}{2}$,x2=$\frac{5}{2}$ | D. | x1=-4,x2=0 |
分析 二次函数y=ax2+1的图象经过点(-2,0),得到4a+1=0,求得a=-$\frac{1}{4}$,代入方程a(x-2)2+1=0即可得到结论.
解答 解:∵二次函数y=ax2+1的图象经过点(-2,0),
∴4a+1=0,
∴a=-$\frac{1}{4}$,
∴方程a(x-2)2+1=0为:方程-$\frac{1}{4}$(x-2)2+1=0,
解得:x1=0,x2=4,
故选A.
点评 本题考查了二次函数与x轴的交点问题,一元二次方程的解,正确的理解题意是解题的关键.

练习册系列答案
相关题目
8.四张完全相同的卡片上,分别画有圆、正方形、等边三角形和线段,现从中随机抽取两张,卡片上画的恰好都是中心对称图形的概率为( )
| A. | 1 | B. | $\frac{3}{4}$ | C. | $\frac{1}{2}$ | D. | $\frac{1}{4}$ |
2.下列各式计算正确的是( )
| A. | 4a-a=3 | B. | a6÷a2=a3 | C. | (-a3)2=a6 | D. | a3•a2=a6 |
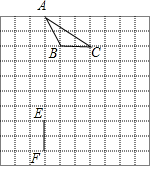 如图,在8×8的正方形网格中,△ABC的顶点和线段EF的端点都在边长为1的小正方形的格点上.请你在图中找出一点D(仅一个点即可),连结DE,DF,使△DEF与△ABC全等,并给予证明.
如图,在8×8的正方形网格中,△ABC的顶点和线段EF的端点都在边长为1的小正方形的格点上.请你在图中找出一点D(仅一个点即可),连结DE,DF,使△DEF与△ABC全等,并给予证明.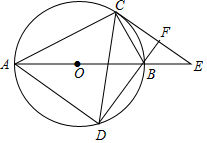 如图,四边形ABCD是⊙O的内接四边形,AB为直径,弦CA=CD,AB=5,BD=3,过C作CE⊥DB,垂足为F,交AB的延长线于E.
如图,四边形ABCD是⊙O的内接四边形,AB为直径,弦CA=CD,AB=5,BD=3,过C作CE⊥DB,垂足为F,交AB的延长线于E.
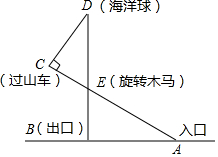 某游乐场部分平面图如图所示,C、E、A在同一直线上,D、E、B在同一直线上,测得A处与E处的距离为80 米,C处与D处的距离为34米,∠C=90°,∠ABE=90°,∠BAE=30°.($\sqrt{2}$≈1.4,$\sqrt{3}$≈1.7)
某游乐场部分平面图如图所示,C、E、A在同一直线上,D、E、B在同一直线上,测得A处与E处的距离为80 米,C处与D处的距离为34米,∠C=90°,∠ABE=90°,∠BAE=30°.($\sqrt{2}$≈1.4,$\sqrt{3}$≈1.7)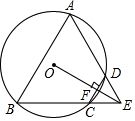 如图,四边形ABCD是⊙O的内接四边形,BC的延长线与AD的延长线交于点E,若AB=BE.
如图,四边形ABCD是⊙O的内接四边形,BC的延长线与AD的延长线交于点E,若AB=BE.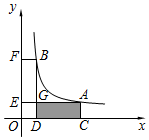 如图,A(a,b),B(1,4)(a>1)是反比例函数y=$\frac{k}{x}$(x>0)图象上两点,过A,B分别作x轴、y轴的垂线,垂足分别为C,D,E,F,AE,BD交于点G.则四边形ACDG的面积随着a的增大( )
如图,A(a,b),B(1,4)(a>1)是反比例函数y=$\frac{k}{x}$(x>0)图象上两点,过A,B分别作x轴、y轴的垂线,垂足分别为C,D,E,F,AE,BD交于点G.则四边形ACDG的面积随着a的增大( )