题目内容
4.解一元一次不等式组$\left\{\begin{array}{l}{1+x>-2}\\{\frac{2x-1}{3}≤1}\end{array}\right.$.分析 先求出每个不等式的解集,再根据找不等式组解集的规律找出不等式组的解集即可.
解答 解:$\left\{\begin{array}{l}{1+x>-2①}\\{\frac{2x-1}{3}≤1②}\end{array}\right.$
∵解不等式①得:x>-3,
解不等式②得:x≤2,
∴不等式组的解集为-3<x≤2.
点评 本题考查了解一元一次不等式组的应用,能根据不等式的解集找出不等式组的解集是解此题的关键.

练习册系列答案
 期末冲刺100分创新金卷完全试卷系列答案
期末冲刺100分创新金卷完全试卷系列答案
相关题目
13.已知二次函数y=ax2-bx+$\frac{1}{2}$b-a与x轴交于A、B两点,则线段AB的最小值为( )
| A. | $\frac{1}{2}$ | B. | 2 | C. | $\sqrt{3}$ | D. | 无法确定 |
14. 如图是正方体的展开图,原正方体相对两个面上的数字和最大是( )
如图是正方体的展开图,原正方体相对两个面上的数字和最大是( )
 如图是正方体的展开图,原正方体相对两个面上的数字和最大是( )
如图是正方体的展开图,原正方体相对两个面上的数字和最大是( )| A. | 7 | B. | 8 | C. | 9 | D. | 10 |
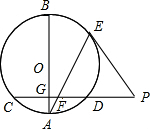 如图,AB是圆O的一条直径,弦CD垂直于AB,垂足为点G、E是劣弧BD上一点,点E处的切线与CD的延长线交于点P,连接AE,交CD于点F.
如图,AB是圆O的一条直径,弦CD垂直于AB,垂足为点G、E是劣弧BD上一点,点E处的切线与CD的延长线交于点P,连接AE,交CD于点F.