Question

6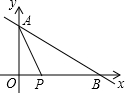．如图，已知一次函数y=-$\frac{1}{2}$x+4与两坐标轴分別交于A、B两点，动点P从原点0出发，以每秒2个单位的速度沿x轴正方向运动，连接AP，设运动时间为ts．
（1）当t为何值时，△PAB的面积为6？
（2）若t＜4，作△PAB中AP边上的高BQ，问：当t为何值时，BQ长为4？并直接写出此时Q的坐标．

Answer 1

分析 （1）先求出AB两点的坐标，再分点P在B点左侧与右侧两种情况进行讨论即可；
（2）作△PAB中AP边上的高BQ，先根据AAS定理得出△AOP≌△BQP，再由勾股定理得出t的值，进而可得出结论．

解答 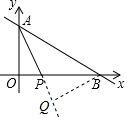解：（1）∵当x=0时，y=4；当y=0时，x=8，
∴A（0，4），B（8，0）．
∵△PAB的面积为6，
∴PB=3．
∵OP=2t，
∴当点P在点B的左侧时，PB=8-2t；当点P在点B的右侧时，PB=2t，
∴t=$\frac{5}{2}$或t=$\frac{11}{2}$；

（2）作△PAB中AP边上的高BQ，
在△AOP与△BQP中，
∵$\left\{\begin{array}{l}{∠AOP=∠BQP}\\{∠APO=∠BPQ}\\{AO=BQ}\end{array}\right.$，
∴△AOP≌△BQP（AAS），
∴AP=BP．
在Rt△AOP中，
∵OP²+OA²=AP²，即4²+（2t）²=（8-2t）²，解得t=$\frac{3}{2}$，
∴当t=$\frac{3}{2}$时，BQ的长为4，
∴Q（$\frac{24}{5}$，-$\frac{12}{5}$）．

点评 本题考查的是一次函数图象上点的坐标特点，熟知一次函数图象上各点的坐标一定适合此函数的解析式是解答此题的关键．