题目内容
15．计算（1）$\frac{\sqrt{8}-\sqrt{18}}{\sqrt{2}}$
（2）（3+$\sqrt{5}$）（$\sqrt{5}$-2）+5$\sqrt{\frac{1}{5}}$-$\sqrt{20}$．
分析 （1）计算时先把二次根式化简为最简二次根式，再合并同类二次根式，最后进行约分；
（2）先去括号，再合并同类二次根式．
解答 解：（1）$\frac{\sqrt{8}-\sqrt{18}}{\sqrt{2}}$，
=$\frac{2\sqrt{2}-3\sqrt{2}}{\sqrt{2}}$，
=$\frac{-\sqrt{2}}{\sqrt{2}}$，
=-1；
（2）（3+$\sqrt{5}$）（$\sqrt{5}$-2）+5$\sqrt{\frac{1}{5}}$-$\sqrt{20}$，
=3$\sqrt{5}$-6+5-2$\sqrt{5}$+5×$\frac{\sqrt{5}}{5}$-2$\sqrt{5}$，
=3$\sqrt{5}$-2$\sqrt{5}$-2$\sqrt{5}$+$\sqrt{5}$-1，
=-1．
点评 本题考查了二次根式的混合计算，正确化简是解题的关键．
练习册系列答案
相关题目
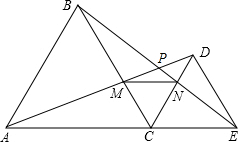如图，点C为线段AE上任意一点，在AE同侧分别作等边三角形△ABC和等边三角形△CDE，连接AD，BE分别交BC，CD于点M，N，连接MN，则下列结论：
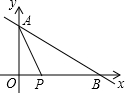如图，已知一次函数y=-$\frac{1}{2}$x+4与两坐标轴分別交于A、B两点，动点P从原点0出发，以每秒2个单位的速度沿x轴正方向运动，连接AP，设运动时间为ts．
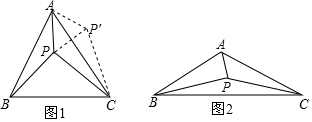在△ABC中，AB=AC，∠BAC=α，点P是△ABC内一点，且∠PAC+∠PCA=$\frac{α}{2}$，连接PB，试探究PA、PB、PC满足的等量关系．
如图，抛物线y=a（x-1）2+k与x轴交于A、C两点，与y轴交于点B，点A、B的坐标分别为（-1，0）和（0，3）．
已知：如图，?ABCD的两条对角线相交于点O，E是BO的中点．过点B作AC的平行线BF，交CE的延长线于点F，连接AF．