题目内容
8．先化简，再求值：（$\frac{1}{x-1}-x+1$）$÷\frac{2x-4}{1-x}$，其中x=$\frac{3}{2}$．分析 先算减法，再算除法，最后把x的值代入进行计算即可．
解答 解：原式=$\frac{1-（x-1）^{2}}{x-1}$•$\frac{-（x-1）}{2（x-2）}$
=$\frac{1-{x}^{2}-1+2x}{x-1}$•$\frac{-（x-1）}{2（x-2）}$
=$\frac{-x（x-2）}{x-1}$•$\frac{-（x-1）}{2（x-2）}$
=$\frac{x}{2}$，
当x=$\frac{3}{2}$时，原式=$\frac{3}{4}$．
点评 本题考查的是分式的化简求值，熟知分式混合运算的法则是解答此题的关键．
练习册系列答案
相关题目
如图所示，在△ABC中，∠CAB=70°，在同一平面内，将△ABC绕A点逆时针旋转到△AB′C′的位置，使CC′∥AB，则∠BAB′=40°．
如图，在△ABC中，AB=AC，点O在边AB上，⊙O过点B且分别与边AB、BC相交于点D、E，EF为⊙O的切线，交AC于点F．
3．假设你班有男生24名，女生26名，班主任要从班里任选一名“社区服务”志愿者，则选中男生的概率是（ ）
| A． | $\frac{12}{25}$ | B． | $\frac{13}{25}$ | C． | $\frac{1}{2}$ | D． | $\frac{1}{50}$ |
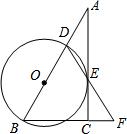在△ABC中，∠ACB=90°，D是AB边上一点，以BD为直径的⊙O与边AC有公共点E，连结DE并延长，与BC的延长线交于点F，BD=BF．
20．$\frac{1}{2}$sin60°的值等于（ ）
| A． | $\frac{1}{4}$ | B． | $\frac{1}{2}$ | C． | $\frac{{\sqrt{3}}}{4}$ | D． | $\sqrt{3}$ |
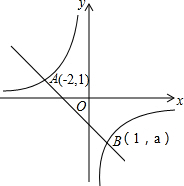如图，一次函数y=kx+b的图象与反比例函数y=$\frac{a}{x}$的图象相交于A、B两点．