题目内容
19.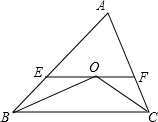 如图所示,BO平分∠CBA,CO平分∠ACB,过O作EF∥BC,若AB=12,AC=8,求△AEF的周长.
如图所示,BO平分∠CBA,CO平分∠ACB,过O作EF∥BC,若AB=12,AC=8,求△AEF的周长.
分析 根据角平分线的定义可得∠OBE=∠OBC,∠OCF=∠OCB,再根据两直线平行,内错角相等可得∠OBC=∠BOE,∠OCB=∠COF,然后求出∠OBE=∠BOE,∠OCF=∠COF,再根据等角对等边可得OE=BE,OF=CF,即可得证.
解答 解:∵BO平分∠CBA,
∴∠EBO=∠OBC,
∵CO平分∠ACB,
∴∠FCO=∠OCB,
∵EF∥BC,
∴∠EOB=∠OBC,∠FOC=∠OCB,
∴∠EBO=∠EOB,∠FOC=∠FCO,
∴BE=OE,CF=OF,
∴△AEF的周长=AE+OE+OF+AF=AE+BE+CF+AF=AB+AC,
∵AB=12,AC=8,
∴C△AEF=12+8=20.
点评 本题考查了等腰三角形的判定与性质,平行线的性质,主要利用了角平分线的定义,等角对等边的性质,两直线平行,内错角相等的性质,熟记各性质是解题的关键

练习册系列答案
 举一反三同步巧讲精练系列答案
举一反三同步巧讲精练系列答案 口算与应用题卡系列答案
口算与应用题卡系列答案 名师点睛字词句段篇系列答案
名师点睛字词句段篇系列答案
相关题目
10. 如图,AC⊥BC,且BC=6,AC=8,AB=10,则点B到AC的距离是( )
如图,AC⊥BC,且BC=6,AC=8,AB=10,则点B到AC的距离是( )
 如图,AC⊥BC,且BC=6,AC=8,AB=10,则点B到AC的距离是( )
如图,AC⊥BC,且BC=6,AC=8,AB=10,则点B到AC的距离是( )| A. | 6 | B. | 7 | C. | 8 | D. | 10 |
4.已知抛物线y=ax2与双曲线y=-$\frac{2}{x}$交点的横坐标大于0,则a的取值范围是( )
| A. | a>0 | B. | a<0 | C. | a>-2 | D. | a<-2 |
 数a,b在数轴上对应点A,B的位置如图所示,且|a|=2,b是16的一个平方根,求式子|a+b|-$\sqrt{{a}^{2}}$-$\root{3}{(a-b)^{3}}$的值.
数a,b在数轴上对应点A,B的位置如图所示,且|a|=2,b是16的一个平方根,求式子|a+b|-$\sqrt{{a}^{2}}$-$\root{3}{(a-b)^{3}}$的值.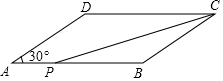 如图,在?ABCD中,AB=8cm,BC=6cm,∠A=30°,点P从点A出发沿线段AB以1m/s的速度向B点移动.
如图,在?ABCD中,AB=8cm,BC=6cm,∠A=30°,点P从点A出发沿线段AB以1m/s的速度向B点移动. 如图,D是△ABC的BA边延长线上的一点,AE是∠DAC的平分线,∠B=∠C,试说明:AE∥BC.
如图,D是△ABC的BA边延长线上的一点,AE是∠DAC的平分线,∠B=∠C,试说明:AE∥BC. 如图,Rt△ABC中,∠C=90°,用直尺和圆规在边BC上找一点D,使D到AB的距离等于CD.(保留作图痕迹,不写作法)
如图,Rt△ABC中,∠C=90°,用直尺和圆规在边BC上找一点D,使D到AB的距离等于CD.(保留作图痕迹,不写作法)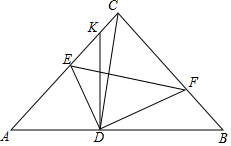 如图,已知在等腰Rt△ABC中,∠C=90°,AB=6,若将△ABC翻折,且点C落在AB边上点D处,折痕EF分别交边AC,BC于点E和点F,过点D作DK⊥AB,交射线AC于点K.
如图,已知在等腰Rt△ABC中,∠C=90°,AB=6,若将△ABC翻折,且点C落在AB边上点D处,折痕EF分别交边AC,BC于点E和点F,过点D作DK⊥AB,交射线AC于点K.