题目内容
10. 如图,AC⊥BC,且BC=6,AC=8,AB=10,则点B到AC的距离是( )
如图,AC⊥BC,且BC=6,AC=8,AB=10,则点B到AC的距离是( )| A. | 6 | B. | 7 | C. | 8 | D. | 10 |
分析 利用勾股定理逆定理判断出△ABC是直角三角形,∠C=90°,再根据点到直线的距离的定义解答.
解答 解:∵BC2+AC2=62+82=100,
AB2=102=100,
∴BC2+AC2=AB2,
根据勾股定理逆定理得,△ABC是直角三角形,∠C=90°,
所以,点B到AC的距离是6.
故选A.
点评 本题考查了勾股定理逆定理,点到直线的距离的定义,熟记定理并判断出三角形是直角三角形是解题的关键.

练习册系列答案
 高中必刷题系列答案
高中必刷题系列答案
相关题目
3.若α与β互余,且α:β=3:2,那么α的度数是( )
| A. | 18° | B. | 36° | C. | 54° | D. | 108° |
1.某班九年级第二学期数学一共进行四次考试,小丽和小明的成绩如表所示:
(1)请你通过计算这四次考试成绩的方差,比较谁的成绩比较稳定?
(2)若老师计算学生的学期总评成绩按照如下的标准:单元测验1占10%,期中考试占30%,单元测验2占10%,期末考试成绩占50%.请你通过计算,比较谁的学期总评成绩高?
| 学生 | 单元测验1 | 期中考试 | 单元测验2 | 期未考试 |
| 小丽 | 85 | 75 | 95 | 85 |
| 小明 | 65 | 95 | 85 | 95 |
(2)若老师计算学生的学期总评成绩按照如下的标准:单元测验1占10%,期中考试占30%,单元测验2占10%,期末考试成绩占50%.请你通过计算,比较谁的学期总评成绩高?
5.方程x(x-4)=0的根是( )
| A. | x1=0,x2=4 | B. | x1=0,x2=-4 | C. | x1=1,x2=4 | D. | x1=1,x2=-4 |
18.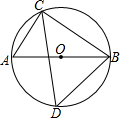 如图,⊙O是锐角△CBD的外接圆,AB是⊙O的直径,连结AC,若∠DCB=θ,则CD与AC,BC,θ关系正确的是( )
如图,⊙O是锐角△CBD的外接圆,AB是⊙O的直径,连结AC,若∠DCB=θ,则CD与AC,BC,θ关系正确的是( )
 如图,⊙O是锐角△CBD的外接圆,AB是⊙O的直径,连结AC,若∠DCB=θ,则CD与AC,BC,θ关系正确的是( )
如图,⊙O是锐角△CBD的外接圆,AB是⊙O的直径,连结AC,若∠DCB=θ,则CD与AC,BC,θ关系正确的是( )| A. | CD=(AC+BC)sinθ | B. | CD=(AC+BC)cosθ | ||
| C. | CD=AC•cosθ+BC•sinθ | D. | CD=AC•sinθ+BC•cosθ |
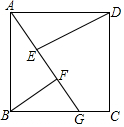 已知:如图,四边形ABCD是正方形,G是BC上的一点,DE⊥AG,BF⊥AG,垂足分别为E、F.
已知:如图,四边形ABCD是正方形,G是BC上的一点,DE⊥AG,BF⊥AG,垂足分别为E、F.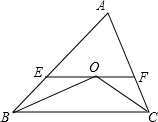 如图所示,BO平分∠CBA,CO平分∠ACB,过O作EF∥BC,若AB=12,AC=8,求△AEF的周长.
如图所示,BO平分∠CBA,CO平分∠ACB,过O作EF∥BC,若AB=12,AC=8,求△AEF的周长.