题目内容
14.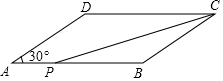 如图,在?ABCD中,AB=8cm,BC=6cm,∠A=30°,点P从点A出发沿线段AB以1m/s的速度向B点移动.
如图,在?ABCD中,AB=8cm,BC=6cm,∠A=30°,点P从点A出发沿线段AB以1m/s的速度向B点移动.(1)当P点运动了几秒时,△PBC为等腰三角形?
(2)是否存在一点P,使S△PBC=$\frac{1}{3}$S?ABCD?若存在求AP的长,若不存在,请说明理由.
分析 (1)由等腰三角形的性质得出BP=BC=6,得出AP=AB-BP=8-6=2,求出t=2即可;
(2)由平行四边形的性质得出AD=BC=6cm,过D作DH⊥AB于H,由含30°角的直角三角形的性质得出DH=$\frac{1}{2}$AD=3cm,求出?ABCD的面积=AB•DH=24,得出△PBC的面积=$\frac{1}{2}$BP•DH=8,求出BP=$\frac{16}{3}$cm,即可得出AP的长.
解答 解:(1)∵△PBC是等腰三角形,
∴BP=BC=6,
∴AP=AB-BP=8-6=2,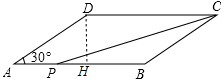
∴t=2,
即当P点运动了2秒时,△PBC为等腰三角形;
(2)∵四边形ABCD是平行四边形,
∴AD=BC=6cm,过D作DH⊥AB于H,
∵∠A=30°,
∴DH=$\frac{1}{2}$AD=3cm,
∴?ABCD的面积=AB•DH=8×3=24,
∴△PBC的面积=$\frac{1}{3}$×24=8=$\frac{1}{2}$BP•DH,
∴BP=$\frac{16}{3}$,
∴AP=AB-BP=8-$\frac{16}{3}$=$\frac{8}{3}$(cm).
点评 本题考查了平行四边形的性质、等腰三角形的性质、含30°角的直角三角形的性质等知识;熟练掌握平行四边形的性质是解决问题的关键.

练习册系列答案
 教材全解字词句篇系列答案
教材全解字词句篇系列答案
相关题目
5.下列计算正确的是( )
| A. | $\sqrt{3}$×$\sqrt{2}$=6 | B. | $\sqrt{12}$-$\sqrt{3}$=$\sqrt{3}$ | C. | $\sqrt{3}$+$\sqrt{2}$=$\sqrt{5}$ | D. | $\sqrt{8}$÷$\sqrt{2}$=4 |
5.方程x(x-4)=0的根是( )
| A. | x1=0,x2=4 | B. | x1=0,x2=-4 | C. | x1=1,x2=4 | D. | x1=1,x2=-4 |
1.已知A(2,y1),B(-3,y2),C(-5,y3)三个点都在反比例函数y=-$\frac{7}{x}$的图象上,比较y1,y2,y3的大小,则下列各式正确的是( )
| A. | y1<y2<y3 | B. | y1<y3<y2 | C. | y2<y3<y1 | D. | y3<y2<y1 |
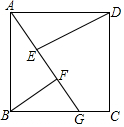 已知:如图,四边形ABCD是正方形,G是BC上的一点,DE⊥AG,BF⊥AG,垂足分别为E、F.
已知:如图,四边形ABCD是正方形,G是BC上的一点,DE⊥AG,BF⊥AG,垂足分别为E、F. 如图,已知直线AB、CD、EF交于O点,∠AOE=45°,∠DOF=30°,求∠BOC的度数.
如图,已知直线AB、CD、EF交于O点,∠AOE=45°,∠DOF=30°,求∠BOC的度数.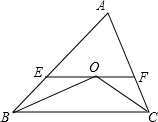 如图所示,BO平分∠CBA,CO平分∠ACB,过O作EF∥BC,若AB=12,AC=8,求△AEF的周长.
如图所示,BO平分∠CBA,CO平分∠ACB,过O作EF∥BC,若AB=12,AC=8,求△AEF的周长. 如图,将纸片△ABC沿DE折叠,点A落在△ABC的形内,已知∠1+∠2=102°,则∠A的大小等于51度.
如图,将纸片△ABC沿DE折叠,点A落在△ABC的形内,已知∠1+∠2=102°,则∠A的大小等于51度.