题目内容
8.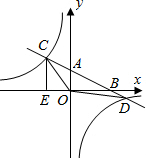 如图,在平面直角坐标系中,O为原点,直线AB分别与x轴、y轴交于B和A,与反比例函数的图象交于C、D,CE⊥x轴于点E,tan∠ABO=$\frac{1}{2}$,OB=4,OE=2.
如图,在平面直角坐标系中,O为原点,直线AB分别与x轴、y轴交于B和A,与反比例函数的图象交于C、D,CE⊥x轴于点E,tan∠ABO=$\frac{1}{2}$,OB=4,OE=2.(1)求直线AB和反比例函数的解析式;
(2)求△OCD的面积.
分析 (1)根据已知条件求出A、B、C点坐标,用待定系数法求出直线AB和反比例的函数解析式;
(2)联立一次函数的解析式和反比例的函数解析式可得交点D的坐标,从而根据三角形面积公式求解.
解答 解:(1)∵OB=4,OE=2,
∴BE=2+4=6.
∵CE⊥x轴于点E,tan∠ABO=$\frac{AO}{BO}$=$\frac{CE}{BE}$=$\frac{1}{2}$.
∴OA=2,CE=3.
∴点A的坐标为(0,2)、点B的坐标为C(4,0)、点C的坐标为(-2,3).
设直线AB的解析式为y=kx+b,则$\left\{\begin{array}{l}{0+b=2}\\{4k+b=0}\end{array}\right.$,
解得$\left\{\begin{array}{l}{k=-\frac{1}{2}}\\{b=2}\end{array}\right.$.
故直线AB的解析式为y=-$\frac{1}{2}$x+2.
设反比例函数的解析式为y=$\frac{m}{x}$(m≠0),
将点C的坐标代入,得3=$\frac{m}{-2}$,
∴m=-6.
∴该反比例函数的解析式为y=-$\frac{6}{x}$.
(2)联立反比例函数的解析式和直线AB的解析式可得$\left\{\begin{array}{l}{y=-\frac{6}{x}}\\{y=-\frac{1}{2}x+2}\end{array}\right.$,
可得交点D的坐标为(6,-1),
则△BOD的面积=4×1÷2=2,
△BOC的面积=4×3÷2=6,
故△OCD的面积为2+6=8.
点评 本题是一次函数与反比例函数的综合题.主要考查待定系数法求函数解析式.求A、B、C点的坐标需用正切定义或相似三角形的性质,起点稍高,部分学生感觉较难.

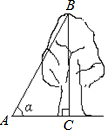 如图,在地面上的点A处测得树顶B的仰角为α度,若AC=6米,则树高BC为( )
如图,在地面上的点A处测得树顶B的仰角为α度,若AC=6米,则树高BC为( )| A. | 6sinα米 | B. | 6tanα米 | C. | $\frac{6}{tanα}$米 | D. | $\frac{6}{cosα}$米 |
 如图,把矩形纸片OABC放在平面直角坐标系中,使OA、OC分别落在x轴正半轴、y轴正半轴上,将纸片沿AC折叠,得到点B的对应点B′.若OA=2,OC=3,则点B′的坐标为(-$\frac{10}{13}$,$\frac{15}{13}$).
如图,把矩形纸片OABC放在平面直角坐标系中,使OA、OC分别落在x轴正半轴、y轴正半轴上,将纸片沿AC折叠,得到点B的对应点B′.若OA=2,OC=3,则点B′的坐标为(-$\frac{10}{13}$,$\frac{15}{13}$).
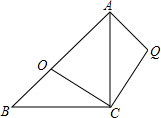 如图,等腰直角△ABC中,AC=BC,∠ACB=90°,点O分斜边AB为BO:OA=1:$\sqrt{3}$,将△BOC绕C点顺时针方向旋转到△AQC的位置,则∠AQC=105°.
如图,等腰直角△ABC中,AC=BC,∠ACB=90°,点O分斜边AB为BO:OA=1:$\sqrt{3}$,将△BOC绕C点顺时针方向旋转到△AQC的位置,则∠AQC=105°.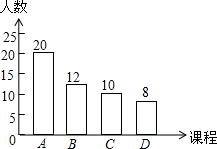 某学校计划开设A,B,C,D四门校本课程供学生选修,规定每个学生必须并且只能选修其中一门,为了了解学生的选修意向,现随机抽取了部分学生进行调查,并将调查结果绘制成如图所示的条形统计图,已知该校学生人数为2000人,由此估计选修A课程的学生有800人.
某学校计划开设A,B,C,D四门校本课程供学生选修,规定每个学生必须并且只能选修其中一门,为了了解学生的选修意向,现随机抽取了部分学生进行调查,并将调查结果绘制成如图所示的条形统计图,已知该校学生人数为2000人,由此估计选修A课程的学生有800人.