题目内容
18.不等式组$\left\{\begin{array}{l}{x+1>0}\\{2x-1≤3}\end{array}\right.$的解集为-1<x≤2.分析 分别求出各不等式的解集,再求出其公共解集即可.
解答 解:$\left\{\begin{array}{l}{x+1>0①}\\{2x-1≤3②}\end{array}\right.$,
由①得,x>-1,
由②得x≤2,
故此不等式组的解集为:-1<x≤2.
故答案为:-1<x≤2.
点评 本题解一元一次不等式组,熟知“同大取大;同小取小;大小小大中间找;大大小小找不到”的法则是解答此题的关键.

练习册系列答案
相关题目
6.点A(-1,y1),B(-2,y2)在反比例函数y=$\frac{2}{x}$的图象上,则y1,y2的大小关系是( )
| A. | y1>y2 | B. | y1=y2 | C. | y1<y2 | D. | 不能确定 |
10.下列运算正确的是( )
| A. | (-a2)•a3=-a6 | B. | a6÷a3=a2 | C. | a2+a3=a5 | D. | (a3)2=a6 |
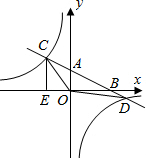 如图,在平面直角坐标系中,O为原点,直线AB分别与x轴、y轴交于B和A,与反比例函数的图象交于C、D,CE⊥x轴于点E,tan∠ABO=$\frac{1}{2}$,OB=4,OE=2.
如图,在平面直角坐标系中,O为原点,直线AB分别与x轴、y轴交于B和A,与反比例函数的图象交于C、D,CE⊥x轴于点E,tan∠ABO=$\frac{1}{2}$,OB=4,OE=2. 如图,在?ABCD中,E、F分别是AB、CD的中点.
如图,在?ABCD中,E、F分别是AB、CD的中点.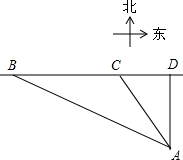 为保护渔民的生命财产安全,我国政府在南海海域新建了一批观测点和避风港.某日在观测点A处发现在其北偏西36.9°的C处有一艘渔船正在作业,同时检测到在渔船的正西B处有一股强台风正以每小时40海里的速度向正东方向移动,于是马上通知渔船到位于其正东方向的避风港D处进行躲避.已知避风港D在观测点A的正北方向,台风中心B在观测点A的北偏西67.5°的方向,渔船C与观测点A相距350海里,台风中心的影响半径为200海里,渔船的速度为每小时18海里,问渔船能否顺利躲避本次台风的影响?(sin36.9°≈0.6,tan36.9≈0.75,sin67.5≈0.92,tan67.5≈2.4)
为保护渔民的生命财产安全,我国政府在南海海域新建了一批观测点和避风港.某日在观测点A处发现在其北偏西36.9°的C处有一艘渔船正在作业,同时检测到在渔船的正西B处有一股强台风正以每小时40海里的速度向正东方向移动,于是马上通知渔船到位于其正东方向的避风港D处进行躲避.已知避风港D在观测点A的正北方向,台风中心B在观测点A的北偏西67.5°的方向,渔船C与观测点A相距350海里,台风中心的影响半径为200海里,渔船的速度为每小时18海里,问渔船能否顺利躲避本次台风的影响?(sin36.9°≈0.6,tan36.9≈0.75,sin67.5≈0.92,tan67.5≈2.4) 如图,请你以y轴为对称轴画出所给图的另一半,若点A坐标为(-3,3),写出点A的对应点的坐标,并说明完成后的图形可能代表的含义.
如图,请你以y轴为对称轴画出所给图的另一半,若点A坐标为(-3,3),写出点A的对应点的坐标,并说明完成后的图形可能代表的含义.