题目内容
13.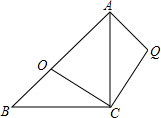 如图,等腰直角△ABC中,AC=BC,∠ACB=90°,点O分斜边AB为BO:OA=1:$\sqrt{3}$,将△BOC绕C点顺时针方向旋转到△AQC的位置,则∠AQC=105°.
如图,等腰直角△ABC中,AC=BC,∠ACB=90°,点O分斜边AB为BO:OA=1:$\sqrt{3}$,将△BOC绕C点顺时针方向旋转到△AQC的位置,则∠AQC=105°.
分析 连接OQ,由旋转的性质可知:△AQC≌△BOC,从而推出∠OAQ=90°,∠OCQ=90°,再根据特殊直角三角形边的关系,分别求出∠AQO与∠OQC的值,可求出结果.
解答  解:连接OQ,
解:连接OQ,
∵AC=BC,∠ACB=90°,
∴∠BAC=∠B=45°,
由旋转的性质可知:△AQC≌△BOC,
∴AQ=BO,CQ=CO,∠QAC=∠B=45°,∠ACQ=∠BCO,
∴∠OAQ=∠BAC+∠CAQ=90°,∠OCQ=∠OCA+∠ACQ=∠OCA+∠BCO=90°,
∴∠OQC=45°,
∵BO:OA=1:$\sqrt{3}$,
设BO=1,OA=$\sqrt{3}$,
∴AQ=1,则tan∠AQO=$\frac{AO}{AQ}$=$\sqrt{3}$,
∴∠AQO=60°,
∴∠AQC=105°.
点评 本题主要考查了图形旋转的性质,特殊角直角三角形的边角关系,掌握图形旋转的性质,熟记特殊直角三角形的边角关系是解决问题的关键.

练习册系列答案
相关题目
4.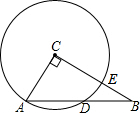 如图,在Rt△ABC中,∠ACB=90°,AC=3,BC=4,以点C为圆心,CA为半径的圆与AB交于点D,则AD的长为( )
如图,在Rt△ABC中,∠ACB=90°,AC=3,BC=4,以点C为圆心,CA为半径的圆与AB交于点D,则AD的长为( )
 如图,在Rt△ABC中,∠ACB=90°,AC=3,BC=4,以点C为圆心,CA为半径的圆与AB交于点D,则AD的长为( )
如图,在Rt△ABC中,∠ACB=90°,AC=3,BC=4,以点C为圆心,CA为半径的圆与AB交于点D,则AD的长为( )| A. | $\frac{18}{5}$ | B. | $\frac{5}{2}$ | C. | $\frac{24}{5}$ | D. | $\frac{9}{5}$ |
18.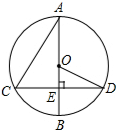 如图,在⊙O中,直径AB⊥CD,垂足为E,∠BOD=48°,则∠BAC的大小是( )
如图,在⊙O中,直径AB⊥CD,垂足为E,∠BOD=48°,则∠BAC的大小是( )
 如图,在⊙O中,直径AB⊥CD,垂足为E,∠BOD=48°,则∠BAC的大小是( )
如图,在⊙O中,直径AB⊥CD,垂足为E,∠BOD=48°,则∠BAC的大小是( )| A. | 60° | B. | 48° | C. | 30° | D. | 24° |
2.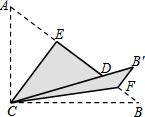 如图,Rt△ABC中,∠ACB=90°,AC=3,BC=4,将边AC沿CE翻折,使点A落在AB上的点D处;再将边BC沿CF翻折,使点B落在CD的延长线上的点B′处,两条折痕与斜边AB分别交于点E、F,则线段B′F的长为( )
如图,Rt△ABC中,∠ACB=90°,AC=3,BC=4,将边AC沿CE翻折,使点A落在AB上的点D处;再将边BC沿CF翻折,使点B落在CD的延长线上的点B′处,两条折痕与斜边AB分别交于点E、F,则线段B′F的长为( )
 如图,Rt△ABC中,∠ACB=90°,AC=3,BC=4,将边AC沿CE翻折,使点A落在AB上的点D处;再将边BC沿CF翻折,使点B落在CD的延长线上的点B′处,两条折痕与斜边AB分别交于点E、F,则线段B′F的长为( )
如图,Rt△ABC中,∠ACB=90°,AC=3,BC=4,将边AC沿CE翻折,使点A落在AB上的点D处;再将边BC沿CF翻折,使点B落在CD的延长线上的点B′处,两条折痕与斜边AB分别交于点E、F,则线段B′F的长为( )| A. | $\frac{3}{5}$ | B. | $\frac{4}{5}$ | C. | $\frac{2}{3}$ | D. | $\frac{\sqrt{3}}{2}$ |
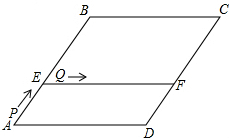 如图,在菱形ABCD中,AB=10,sinA=$\frac{4}{5}$,点E在AB上,AE=4,过点E作EF∥AD,交CD于点F.
如图,在菱形ABCD中,AB=10,sinA=$\frac{4}{5}$,点E在AB上,AE=4,过点E作EF∥AD,交CD于点F.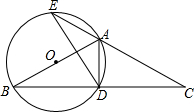 如图,△ABC中,AB=AC,以AB为直径作⊙O,交BC于点D,交CA的延长线于点E,连接AD、DE.
如图,△ABC中,AB=AC,以AB为直径作⊙O,交BC于点D,交CA的延长线于点E,连接AD、DE.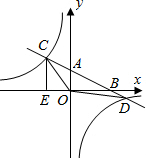 如图,在平面直角坐标系中,O为原点,直线AB分别与x轴、y轴交于B和A,与反比例函数的图象交于C、D,CE⊥x轴于点E,tan∠ABO=$\frac{1}{2}$,OB=4,OE=2.
如图,在平面直角坐标系中,O为原点,直线AB分别与x轴、y轴交于B和A,与反比例函数的图象交于C、D,CE⊥x轴于点E,tan∠ABO=$\frac{1}{2}$,OB=4,OE=2. 如图,AB为⊙O的直径,CO⊥AB于O,D在⊙O上,连接BD,CD,延长CD与AB的延长线交于E,F在BE上,且FD=FE.
如图,AB为⊙O的直径,CO⊥AB于O,D在⊙O上,连接BD,CD,延长CD与AB的延长线交于E,F在BE上,且FD=FE.