题目内容
17.将分式$\frac{{x}^{2}-2x+1}{{x}^{2}-1}$化为最简分式,所得结果是$\frac{x-1}{x+1}$.分析 根据平方差公式和完全平方公式把分子、分母因式分解,再进行约分即可.
解答 解:$\frac{{x}^{2}-2x+1}{{x}^{2}-1}$=$\frac{(x-1)^{2}}{(x+1)(x-1)}$=$\frac{x-1}{x+1}$;
故答案为:$\frac{x-1}{x+1}$.
点评 此题考查了最简分式,用到的知识点是平方差公式和完全平方公式;最简分式的标准是分子,分母中不含有公因式,不能再约分.

练习册系列答案
 孟建平小学滚动测试系列答案
孟建平小学滚动测试系列答案
相关题目
2.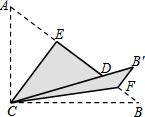 如图,Rt△ABC中,∠ACB=90°,AC=3,BC=4,将边AC沿CE翻折,使点A落在AB上的点D处;再将边BC沿CF翻折,使点B落在CD的延长线上的点B′处,两条折痕与斜边AB分别交于点E、F,则线段B′F的长为( )
如图,Rt△ABC中,∠ACB=90°,AC=3,BC=4,将边AC沿CE翻折,使点A落在AB上的点D处;再将边BC沿CF翻折,使点B落在CD的延长线上的点B′处,两条折痕与斜边AB分别交于点E、F,则线段B′F的长为( )
 如图,Rt△ABC中,∠ACB=90°,AC=3,BC=4,将边AC沿CE翻折,使点A落在AB上的点D处;再将边BC沿CF翻折,使点B落在CD的延长线上的点B′处,两条折痕与斜边AB分别交于点E、F,则线段B′F的长为( )
如图,Rt△ABC中,∠ACB=90°,AC=3,BC=4,将边AC沿CE翻折,使点A落在AB上的点D处;再将边BC沿CF翻折,使点B落在CD的延长线上的点B′处,两条折痕与斜边AB分别交于点E、F,则线段B′F的长为( )| A. | $\frac{3}{5}$ | B. | $\frac{4}{5}$ | C. | $\frac{2}{3}$ | D. | $\frac{\sqrt{3}}{2}$ |
6.点A(-1,y1),B(-2,y2)在反比例函数y=$\frac{2}{x}$的图象上,则y1,y2的大小关系是( )
| A. | y1>y2 | B. | y1=y2 | C. | y1<y2 | D. | 不能确定 |
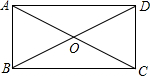 如图所示,在矩形ABCD中,DG⊥AC,G为垂足,∠CDG:∠GDA=1:3,那么∠BDG=45°,若AC=8,那么DG=2$\sqrt{2}$.
如图所示,在矩形ABCD中,DG⊥AC,G为垂足,∠CDG:∠GDA=1:3,那么∠BDG=45°,若AC=8,那么DG=2$\sqrt{2}$.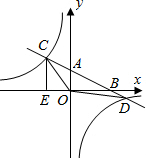 如图,在平面直角坐标系中,O为原点,直线AB分别与x轴、y轴交于B和A,与反比例函数的图象交于C、D,CE⊥x轴于点E,tan∠ABO=$\frac{1}{2}$,OB=4,OE=2.
如图,在平面直角坐标系中,O为原点,直线AB分别与x轴、y轴交于B和A,与反比例函数的图象交于C、D,CE⊥x轴于点E,tan∠ABO=$\frac{1}{2}$,OB=4,OE=2. 如图,AB为⊙O的直径,CO⊥AB于O,D在⊙O上,连接BD,CD,延长CD与AB的延长线交于E,F在BE上,且FD=FE.
如图,AB为⊙O的直径,CO⊥AB于O,D在⊙O上,连接BD,CD,延长CD与AB的延长线交于E,F在BE上,且FD=FE. 如图,在?ABCD中,E、F分别是AB、CD的中点.
如图,在?ABCD中,E、F分别是AB、CD的中点.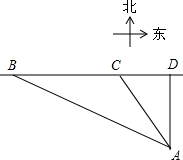 为保护渔民的生命财产安全,我国政府在南海海域新建了一批观测点和避风港.某日在观测点A处发现在其北偏西36.9°的C处有一艘渔船正在作业,同时检测到在渔船的正西B处有一股强台风正以每小时40海里的速度向正东方向移动,于是马上通知渔船到位于其正东方向的避风港D处进行躲避.已知避风港D在观测点A的正北方向,台风中心B在观测点A的北偏西67.5°的方向,渔船C与观测点A相距350海里,台风中心的影响半径为200海里,渔船的速度为每小时18海里,问渔船能否顺利躲避本次台风的影响?(sin36.9°≈0.6,tan36.9≈0.75,sin67.5≈0.92,tan67.5≈2.4)
为保护渔民的生命财产安全,我国政府在南海海域新建了一批观测点和避风港.某日在观测点A处发现在其北偏西36.9°的C处有一艘渔船正在作业,同时检测到在渔船的正西B处有一股强台风正以每小时40海里的速度向正东方向移动,于是马上通知渔船到位于其正东方向的避风港D处进行躲避.已知避风港D在观测点A的正北方向,台风中心B在观测点A的北偏西67.5°的方向,渔船C与观测点A相距350海里,台风中心的影响半径为200海里,渔船的速度为每小时18海里,问渔船能否顺利躲避本次台风的影响?(sin36.9°≈0.6,tan36.9≈0.75,sin67.5≈0.92,tan67.5≈2.4)