题目内容
3.如图①,②,③,用一种大小相等的正多边形密铺成一个“环”,我们称之为环形密铺.但图④,⑤不是我们所说的环形密铺.请你再写出一种可以进行环形密铺的正多边形:正十二边形.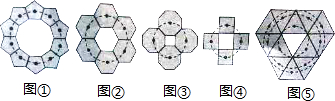
分析 根据环形密铺的定义,所用多边形的外角的2倍是正多边形的内角即可.
解答 解:正十二边形的外角是360°÷12=30°,内角=150°
∵150°×2=300°,
360°-300°=60°,
∴里边是正三角形,
∴正十二边形可以进行环形密铺.
故答案为:正十二边形.
点评 本题考查了平面密铺,观察图形判断出中间空白正多边形的内角是所用正多边形的外角的2倍是解题的关键.

练习册系列答案
相关题目
18.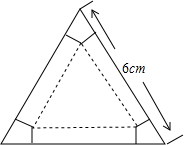 如图,有一块边长为6cm的正三角形纸板,在它的三个角处分别截去一个彼此全等的筝形,再沿图中的虚线折起,做成一个无盖的直三棱柱纸盒,则该纸盒侧面积的最大值是( )
如图,有一块边长为6cm的正三角形纸板,在它的三个角处分别截去一个彼此全等的筝形,再沿图中的虚线折起,做成一个无盖的直三棱柱纸盒,则该纸盒侧面积的最大值是( )
 如图,有一块边长为6cm的正三角形纸板,在它的三个角处分别截去一个彼此全等的筝形,再沿图中的虚线折起,做成一个无盖的直三棱柱纸盒,则该纸盒侧面积的最大值是( )
如图,有一块边长为6cm的正三角形纸板,在它的三个角处分别截去一个彼此全等的筝形,再沿图中的虚线折起,做成一个无盖的直三棱柱纸盒,则该纸盒侧面积的最大值是( )| A. | $\sqrt{3}$cm2 | B. | $\frac{3}{2}$$\sqrt{3}$cm2 | C. | $\frac{9}{2}$$\sqrt{3}$cm2 | D. | $\frac{27}{2}$$\sqrt{3}$cm2 |
15. 如图,直线l外不重合的两点A、B,在直线l上求作一点C,使得AC+BC的长度最短,作法为:①作点B关于直线l的对称点B′;②连接AB′与直线l相交于点C,则点C为所求作的点.在解决这个问题时没有运用到的知识或方法是( )
如图,直线l外不重合的两点A、B,在直线l上求作一点C,使得AC+BC的长度最短,作法为:①作点B关于直线l的对称点B′;②连接AB′与直线l相交于点C,则点C为所求作的点.在解决这个问题时没有运用到的知识或方法是( )
 如图,直线l外不重合的两点A、B,在直线l上求作一点C,使得AC+BC的长度最短,作法为:①作点B关于直线l的对称点B′;②连接AB′与直线l相交于点C,则点C为所求作的点.在解决这个问题时没有运用到的知识或方法是( )
如图,直线l外不重合的两点A、B,在直线l上求作一点C,使得AC+BC的长度最短,作法为:①作点B关于直线l的对称点B′;②连接AB′与直线l相交于点C,则点C为所求作的点.在解决这个问题时没有运用到的知识或方法是( )| A. | 转化思想 | |
| B. | 三角形的两边之和大于第三边 | |
| C. | 两点之间,线段最短 | |
| D. | 三角形的一个外角大于与它不相邻的任意一个内角 |
 如图,已知△ABC.
如图,已知△ABC.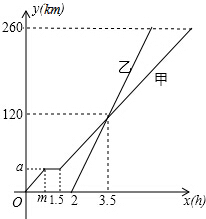 甲、乙两车从A地驶向B地,并以各自的速度匀速行驶,甲车比乙车早行驶2h,并且甲途中休息了0.5h,如图是甲乙两车行驶的距离y(km)与时间x(h)的函数图象,则下列叙述正确的个数为( )
甲、乙两车从A地驶向B地,并以各自的速度匀速行驶,甲车比乙车早行驶2h,并且甲途中休息了0.5h,如图是甲乙两车行驶的距离y(km)与时间x(h)的函数图象,则下列叙述正确的个数为( )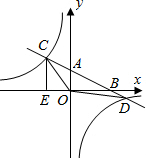 如图,在平面直角坐标系中,O为原点,直线AB分别与x轴、y轴交于B和A,与反比例函数的图象交于C、D,CE⊥x轴于点E,tan∠ABO=$\frac{1}{2}$,OB=4,OE=2.
如图,在平面直角坐标系中,O为原点,直线AB分别与x轴、y轴交于B和A,与反比例函数的图象交于C、D,CE⊥x轴于点E,tan∠ABO=$\frac{1}{2}$,OB=4,OE=2.