题目内容
5.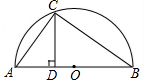 如图是以△ABC的边AB为直径的半圆O,点C恰好在半圆上,过点C作CD⊥AB交AB于点D.若cos∠BCD=$\frac{3}{5}$,AC=4,则BC的长为( )
如图是以△ABC的边AB为直径的半圆O,点C恰好在半圆上,过点C作CD⊥AB交AB于点D.若cos∠BCD=$\frac{3}{5}$,AC=4,则BC的长为( )| A. | 1 | B. | $\frac{16}{3}$ | C. | 3 | D. | $\frac{20}{3}$ |
分析 根据圆周角定理可得∠ACB=90°,然后根据余角的性质可得∠A=∠BCD,利用三角函数可得AD长,进而可利用勾股定理算出CD长,然后再利用三角函数可得BC长.
解答 解:∵AB为直径,
∴∠ACB=90°,
∴∠ACD+∠BCD=90°,
∵CD⊥AB,
∴∠ACD+∠A=90°,
∴∠A=∠BCD,
∵cos∠BCD=$\frac{3}{5}$,
∴cosA=$\frac{3}{5}$,
∵AC=4,
∴AD=$\frac{12}{5}$,
∴CD=$\frac{16}{5}$,
∵cos∠BCD=$\frac{3}{5}$,
∴BC=$\frac{16}{3}$,
故选:B.
点评 此题主要考查了圆周角定理,以及三角函数的应用,关键是掌握半圆(或直径)所对的圆周角是直角,90°的圆周角所对的弦是直径.以及数形结合思想的应用.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
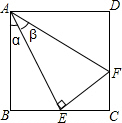 如图,E是正方形ABCD中BC边上的任意一点,连接AE,过点E作EF⊥AE交CD于点F,设∠BAE=α,∠EAF=β.求证:若E是BC的中点,则α=β,AF=AB+CF.
如图,E是正方形ABCD中BC边上的任意一点,连接AE,过点E作EF⊥AE交CD于点F,设∠BAE=α,∠EAF=β.求证:若E是BC的中点,则α=β,AF=AB+CF.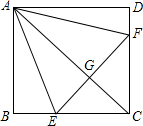 如图,正方形ABCD中,点E、F分别在BC、CD上,△AEF是等边三角形,连接AC交EF于G,求证:
如图,正方形ABCD中,点E、F分别在BC、CD上,△AEF是等边三角形,连接AC交EF于G,求证: