题目内容
1.计算:(1)(-a2)3+(-a3)2-a2•a3
(2)(-$\frac{1}{3}$)-2+(+8)0-22012×(-$\frac{1}{2}$)2011.
(3)a3•(-b3)2+(-$\frac{1}{2}$ab2)3,其中a=$\frac{1}{4}$,b=4.
(4)若2x+5y-3=0,求4x•32y的值.
(5)已知16m=4×22n-2,27n=9×3m+3,求(n-m)2010的值.
分析 (1)原式利用幂的乘方与积的乘方运算法则计算,合并即可得到结果;
(2)原式利用零指数幂、负整数指数幂法则,以及幂的乘方与积的乘方运算法则计算即可得到结果;
(3)原式利用幂的乘方与积的乘方运算法则计算,合并得到最简结果,把a与b的值代入计算即可求出值;
(4)原式变形后,将已知等式变形后代入计算即可求出值;
(5)已知等式变形后,求出m与n的值,代入原式计算即可得到结果.
解答 解:(1)原式=-a6+a6-a5=-a5;
(2)原式=9+1+2=12;
(3)原式=a3b6-$\frac{1}{8}$a3b6=$\frac{7}{8}$a3b6,
当a=$\frac{1}{4}$,b=4时,原式=56;
(4)∵2x+5y-3=0,即2x+5y=3,
∴原式=22x+5y=8;
(5)∵24m=16m=4×22n-2=22n,33n=27n=9×3m+3=3m+5,
∴$\left\{\begin{array}{l}{n=2m}\\{m+5=3n}\end{array}\right.$,
解得:m=1,n=2,即n-m=1,
则原式=1.
点评 此题考查了整式的加减-化简求值,实数的运算,零指数幂、负整数指数幂,熟练掌握去括号法则与合并同类项法则是解本题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
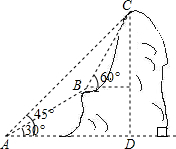 如图,某电信部门计划修建一条连接B、C两地的电缆.测量人员在山脚A点测得B、C两地的仰角分别为30°、45°,在B地测得C地的仰角为60°.已知C地比A地高200m,电缆BC至少长多少米(精确到1m)?
如图,某电信部门计划修建一条连接B、C两地的电缆.测量人员在山脚A点测得B、C两地的仰角分别为30°、45°,在B地测得C地的仰角为60°.已知C地比A地高200m,电缆BC至少长多少米(精确到1m)?
 如图,已知两直线AB、CD相交于点O,EO⊥CD,且∠AOC:∠AOD=1:5.求:
如图,已知两直线AB、CD相交于点O,EO⊥CD,且∠AOC:∠AOD=1:5.求: 如图所示,分别以n边形顶角顶点为圆心,以1cm长为半径画圆,则圆中阴影部分面积之和为πcm2.
如图所示,分别以n边形顶角顶点为圆心,以1cm长为半径画圆,则圆中阴影部分面积之和为πcm2.