题目内容
17.已知一元一次方程k1x+b1=0的解为x=-2,一元一次方程k2x+b2=0的解为x=3,则直线y=k1x+b1与x轴的交点A到直线y=k2x+b2与x轴的交点B之间的距离为( )| A. | 1 | B. | 5 | C. | 6 | D. | 无法确定 |
分析 根据一次函数与一元一次方程的关系,可得点A的坐标为(-2,0),点B的坐标为(3,0),进而求出AB的长度即可.
解答 解:∵一元一次方程k1x+b1=0的解为x=-2,一元一次方程k2x+b2=0的解为x=3,
∴直线y=k1x+b1与x轴的交点A的坐标为(-2,0),直线y=k2x+b2与x轴的交点B的坐标为(3,0),
∴AB=3-(-2)=5.
故选B.
点评 本题考查了一次函数与一元一次方程的关系:方程kx+b=0的解即为直线y=kx+b与x轴交点的横坐标,也考查了两点间的距离.

练习册系列答案
相关题目
5.若y-1与2-x成正比例,则下列说法正确的是( )
| A. | y是x的一次函数 | B. | y是x的正比例函数 | ||
| C. | y是x的函数但不是正比例函数 | D. | y不是x的函数 |
 如图,点A,B,C在⊙O上,若∠ACO=24°,AB∥OC,则∠BOC的度数是48°.
如图,点A,B,C在⊙O上,若∠ACO=24°,AB∥OC,则∠BOC的度数是48°.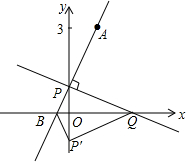 如图,在平面直角坐标系中,O是坐标原点,点A的坐标是(1,3),点P的坐标是(0,b)(b≠0).直线AP交x轴于点B,记点P关于x轴的对称点为P′,点Q为x轴上一动点.
如图,在平面直角坐标系中,O是坐标原点,点A的坐标是(1,3),点P的坐标是(0,b)(b≠0).直线AP交x轴于点B,记点P关于x轴的对称点为P′,点Q为x轴上一动点.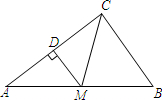 如图,在△ABC中,点M在边AB上,AM=CM,DM⊥AC,且DM∥BC,说明△CMB是等腰三角形.
如图,在△ABC中,点M在边AB上,AM=CM,DM⊥AC,且DM∥BC,说明△CMB是等腰三角形.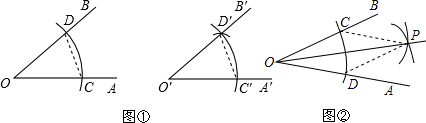
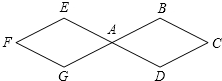 如图,两个连接在一起的菱形的边长都是1cm,一只电子甲虫,从点A开始AGFEADCBAG…的顺序沿菱形的边循环爬行,当电子甲虫爬行1945cm时停下,则它停的位置是点G.
如图,两个连接在一起的菱形的边长都是1cm,一只电子甲虫,从点A开始AGFEADCBAG…的顺序沿菱形的边循环爬行,当电子甲虫爬行1945cm时停下,则它停的位置是点G.