题目内容
 如图,已知:?ABCD中,∠ABC的平分线BG,交AD于G,∠BCD的平分线CE,交BG于F,交AD于E.
如图,已知:?ABCD中,∠ABC的平分线BG,交AD于G,∠BCD的平分线CE,交BG于F,交AD于E.(1)求证:BG⊥CE.
(2)若AB=3,BC=4,求EG的长.
考点:平行四边形的性质
专题:
分析:(1)根据角平分线的性质以及平行四边形的性质得出∠CBG+∠BCE=90°,进而得出BG⊥CE;
(2)根据角平分线的性质以及平行四边形的性质得出∠ABG=∠CBG,则∠AGB=∠ABG,进而求出GD,AE的长,即可得出EG的长.
(2)根据角平分线的性质以及平行四边形的性质得出∠ABG=∠CBG,则∠AGB=∠ABG,进而求出GD,AE的长,即可得出EG的长.
解答:(1)证明:∵?ABCD,
∴AB∥CD,
∴∠ABC+∠BCD=180°,
又∵BG、CE分别是∠ABC和∠BCD的角平分线,
∴∠ABG=∠CBG,∠BCE=∠DCE,
又∵∠ABG+∠CBG+∠BCE+∠DCE=180°,
∴∠CBG+∠BCE=90°,
在△BCF中,∠BFC=180°-∠CBF-∠BCF=90°
即BG⊥CE;
(2)解:∵?ABCD,
∴AD∥BC,AB=CD=3,AD=BC=4,
∴∠AGB=∠CBG,
又∵BG是∠ABC的角平分线,
∴∠ABG=∠CBG,
∴∠AGB=∠ABG,
∴AB=AG=3,
∴GD=AD-AG=4-3=1,
同理:AE=1,
∴EG=AD-AE-GD=4-1-1=2.
∴AB∥CD,
∴∠ABC+∠BCD=180°,
又∵BG、CE分别是∠ABC和∠BCD的角平分线,
∴∠ABG=∠CBG,∠BCE=∠DCE,
又∵∠ABG+∠CBG+∠BCE+∠DCE=180°,
∴∠CBG+∠BCE=90°,
在△BCF中,∠BFC=180°-∠CBF-∠BCF=90°
即BG⊥CE;
(2)解:∵?ABCD,
∴AD∥BC,AB=CD=3,AD=BC=4,
∴∠AGB=∠CBG,
又∵BG是∠ABC的角平分线,
∴∠ABG=∠CBG,
∴∠AGB=∠ABG,
∴AB=AG=3,
∴GD=AD-AG=4-3=1,
同理:AE=1,
∴EG=AD-AE-GD=4-1-1=2.
点评:此题主要考查了平行四边形的性质和角平分线的性质等知识,得出∠AGB=∠ABG是解题关键.

练习册系列答案
相关题目
能判定四边形ABCD为平行四边形的题设是( )
| A、AB=AD,CB=CD |
| B、AB=CD,AD=BC |
| C、∠A=∠B,∠C=∠D |
| D、AB∥CD,AD=BC |
 今年植树节,安庆某中学组织师生开展植树造林活动,为了了解全校1200名学生的植树情况,随机抽样调查50名学生的植树情况,制成如下统计表和条形统计图(均不完整).
今年植树节,安庆某中学组织师生开展植树造林活动,为了了解全校1200名学生的植树情况,随机抽样调查50名学生的植树情况,制成如下统计表和条形统计图(均不完整). 如图,在半径为5cm的⊙O中,直径AB与弦CD相交于点P,∠CAB=50°,∠APD=80°.
如图,在半径为5cm的⊙O中,直径AB与弦CD相交于点P,∠CAB=50°,∠APD=80°. 已知二次函数y=ax2+bx+c(a≠0)的图象经过点A(-1,0),B(-2,0),C(0,-2),直线x=m(m<-2)与x轴交于点D.
已知二次函数y=ax2+bx+c(a≠0)的图象经过点A(-1,0),B(-2,0),C(0,-2),直线x=m(m<-2)与x轴交于点D.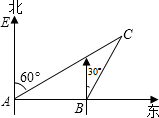 某船以每小时36海里的速度向正东方向航行,在点A测得某岛C在北偏东60°方向上,航行半小时后到达点B,测得该岛在北偏东30°方向上,已知该岛周围16海里内有暗礁.
某船以每小时36海里的速度向正东方向航行,在点A测得某岛C在北偏东60°方向上,航行半小时后到达点B,测得该岛在北偏东30°方向上,已知该岛周围16海里内有暗礁. 如图,△ABC中,DE∥BC,DE=a,AD=b,DB=c,则BC的长是
如图,△ABC中,DE∥BC,DE=a,AD=b,DB=c,则BC的长是