题目内容

如图，△ABC中，DE∥BC，DE=a，AD=b，DB=c，则BC的长是
 
（用a、b、c的代数式表示）．
考点：相似三角形的判定与性质
专题：计算题
分析：根据平行于三角形一边的直线与其他两边所截的三角形与原三角形相似得到△ADE∽△ABC，根据相似的性质得
DE
BC
=
AD
AB
，然后把DE=a，AB=AD+DB=b+c代入计算即可得到BC的长．
解答：解：∵DE∥BC，
∴△ADE∽△ABC，
∴
DE
BC
=
AD
AB
，
而DE=a，AB=AD+DB=b+c，
∴
a
BC
=
b
b+c
，
∴BC=
ab+ac
b
．
故答案为
ab+ac
b
．
点评：本题考查了相似三角形的判定与性质：平行于三角形一边的直线与其他两边所截的三角形与原三角形相似；相似三角形对应边的比相等，都等于相似比．
练习册系列答案
相关题目
如图，已知：?ABCD中，∠ABC的平分线BG，交AD于G，∠BCD的平分线CE，交BG于F，交AD于E．
（1）求证：BG⊥CE．
（2）若AB=3，BC=4，求EG的长．
如图，已知抛物线y=-x2+2x+c经过点C（0，3），且与x轴交于A、B两点（点A在点B的左侧），线段BC与抛物线的对称轴相交于点P．M、N分别是线段OC和x轴上的动点，运动时保持∠MPN=90°不变．
（1）求抛物线的解析式；
（2）①试猜想PN与PM的数量关系，并说明理由；
②在①的前提下，连结MN，设OM=m．△MPN的面积为S，求S的最大值．
今年“五一”黄金周，我省实现社会消费的零售总额约为94亿元．若用科学记数法表示，则94亿可写为
 
元．
已知分式
x2+3x+2
x+2
值为0，那么x的值为
 
．
当m=
 
时，方程x2+（m-2）x-9=0的两个根互为相反数．
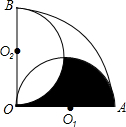如图，扇形OAB的圆心角为90°、半径为2cm，半圆O1和半圆O2的直径分别为OA和OB，则图中阴影部分的面积为
 
cm2．
已知m，n是方程x2-2
2
x+1=0的两根，则代数式
m2+n2+3mn
的值为（　　）
A、3B、5C、9D、±3
当x是不等式组
2x+6＞0
3(x+2)-2＜1
的整数解时，求（
1
x+1
+
x2-2x+1
x2-1
）÷
x-1
x+1
的值．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网