题目内容
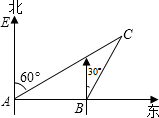 某船以每小时36海里的速度向正东方向航行,在点A测得某岛C在北偏东60°方向上,航行半小时后到达点B,测得该岛在北偏东30°方向上,已知该岛周围16海里内有暗礁.
某船以每小时36海里的速度向正东方向航行,在点A测得某岛C在北偏东60°方向上,航行半小时后到达点B,测得该岛在北偏东30°方向上,已知该岛周围16海里内有暗礁.(1)试说明点B是否在暗礁区域外?
(2)若继续向东航行有无触礁危险?请说明理由.
考点:解直角三角形的应用-方向角问题
专题:
分析:(1)求点B是否在暗礁区域内,其实就是求CB的距离是否大于16,如果大于则不在暗礁区域内,反之则在.可通过构造直角三角形来求CB的长,作CD⊥AB于D点,CD是直角三角形ACD和CBD的公共直角边,可先求出CD的长,再求出CB的长;
(2)本题实际上是问,C到AB的距离即CD是否大于16,如果大于则无触礁危险,反之则有,CD的值,(1)已经求出,只要进行比较即可.
(2)本题实际上是问,C到AB的距离即CD是否大于16,如果大于则无触礁危险,反之则有,CD的值,(1)已经求出,只要进行比较即可.
解答: 解:(1)作CD⊥AB于D点,
解:(1)作CD⊥AB于D点,
设BC为x,
在Rt△BCD中∠CBD=60°,
∴BD=
x.
CD=
x.
在Rt△ACD中∠CAD=30°tan∠CAD=
=
,
∴
=
.
∴x=18.
∴点B是在暗礁区域外;
(2)∵CD=
x=9
,
∵9
<16,
∴若继续向东航行船有触礁的危险.
 解:(1)作CD⊥AB于D点,
解:(1)作CD⊥AB于D点,设BC为x,
在Rt△BCD中∠CBD=60°,
∴BD=
| 1 |
| 2 |
CD=
| ||
| 2 |
在Rt△ACD中∠CAD=30°tan∠CAD=
| CD |
| AD |
| ||
| 3 |
∴
| ||||
18+
|
| ||
| 3 |
∴x=18.
∴点B是在暗礁区域外;
(2)∵CD=
| ||
| 2 |
| 3 |
∵9
| 3 |
∴若继续向东航行船有触礁的危险.
点评:考查了解直角三角形的应用-方向角问题,本题是将实际问题转化为直角三角形中的数学问题,可通过作辅助线构造直角三角形,再把条件和问题转化到这个直角三角形中,使问题解决.

练习册系列答案
相关题目
下列四个图案中,既是轴对称图形又是中心对称图形的有( )
A、 |
B、 |
C、 |
D、 |
 已知抛物线y=ax2+bx+c经过A(3,0)、B(0,3)、C(1,0)三点.
已知抛物线y=ax2+bx+c经过A(3,0)、B(0,3)、C(1,0)三点. 如图,已知:?ABCD中,∠ABC的平分线BG,交AD于G,∠BCD的平分线CE,交BG于F,交AD于E.
如图,已知:?ABCD中,∠ABC的平分线BG,交AD于G,∠BCD的平分线CE,交BG于F,交AD于E.
 如图,抛物线
如图,抛物线 如图,已知抛物线y=-x2+2x+c经过点C(0,3),且与x轴交于A、B两点(点A在点B的左侧),线段BC与抛物线的对称轴相交于点P.M、N分别是线段OC和x轴上的动点,运动时保持∠MPN=90°不变.
如图,已知抛物线y=-x2+2x+c经过点C(0,3),且与x轴交于A、B两点(点A在点B的左侧),线段BC与抛物线的对称轴相交于点P.M、N分别是线段OC和x轴上的动点,运动时保持∠MPN=90°不变.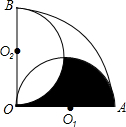 如图,扇形OAB的圆心角为90°、半径为2cm,半圆O1和半圆O2的直径分别为OA和OB,则图中阴影部分的面积为
如图,扇形OAB的圆心角为90°、半径为2cm,半圆O1和半圆O2的直径分别为OA和OB,则图中阴影部分的面积为