题目内容
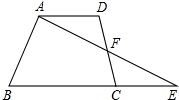 四边形ABCD中,AD∥BC,DF=CF,连接AF并延长交BC延长线于点E.
四边形ABCD中,AD∥BC,DF=CF,连接AF并延长交BC延长线于点E.(1)图中哪两个三角形可以通过怎样的旋转而相互得到?
(2)四边形ABCD的面积与图中哪个三角形的面积相等?
(3)若AB=AD+BC,∠B=70°,试求∠DAF的度数.
考点:旋转的性质
专题:
分析:(1)观察图形可得到△ADF≌△ECF,根据旋转的定义可得出答案;
(2)利用旋转的性质可知S△ADF=S△CEF,再利用面积的和差可得出答案;
(3)根据旋转的性质可得到AB=BE,可求得∠E的度数,即可求得∠DAF的度数.
(2)利用旋转的性质可知S△ADF=S△CEF,再利用面积的和差可得出答案;
(3)根据旋转的性质可得到AB=BE,可求得∠E的度数,即可求得∠DAF的度数.
解答:解:
(1)∵AD∥BC,
∴∠E=∠DAF,且DF=CF,
∴△ADF绕点F旋转180°可得到△ECF;
(2)由(1)可知△ADF≌△ECF,
∴S△ADF=S△CEF,
∴S四边形ABCF+S△ADF=S四边形ABCF+S△CEF,
即S四边形ABCD=S△ABE,
即四边形ABCD的面积和△ABE的面积相等;
(3)∵△ADF≌△ECF,
∴CE=AD,∠E=∠DAF,
∵AB=AD+BC,
∴AB=CE+BC=BE,
∴∠E=∠BAE=
(180°-∠B)=55°,
∴∠DAF=55°.
(1)∵AD∥BC,
∴∠E=∠DAF,且DF=CF,
∴△ADF绕点F旋转180°可得到△ECF;
(2)由(1)可知△ADF≌△ECF,
∴S△ADF=S△CEF,
∴S四边形ABCF+S△ADF=S四边形ABCF+S△CEF,
即S四边形ABCD=S△ABE,
即四边形ABCD的面积和△ABE的面积相等;
(3)∵△ADF≌△ECF,
∴CE=AD,∠E=∠DAF,
∵AB=AD+BC,
∴AB=CE+BC=BE,
∴∠E=∠BAE=
| 1 |
| 2 |
∴∠DAF=55°.
点评:本题主要考查旋转的定义和性质,掌握旋转图形是全等图形是解题的关键.

练习册系列答案
相关题目
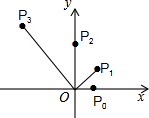 如图,在平面直角坐标系中,已知点P0的坐标为(1,0)将线段OP按逆时针方向旋转45°,再将其长度伸长为OP0的2倍,得到线段OP1,又将线段OP1按逆时针方向旋转45°,再将其长度伸长为OP1的2倍得到线段OP2;…;如此进行下去,得到线段OP3,OP4,…OPn(n为正整数)则点P2015的坐标为( )
如图,在平面直角坐标系中,已知点P0的坐标为(1,0)将线段OP按逆时针方向旋转45°,再将其长度伸长为OP0的2倍,得到线段OP1,又将线段OP1按逆时针方向旋转45°,再将其长度伸长为OP1的2倍得到线段OP2;…;如此进行下去,得到线段OP3,OP4,…OPn(n为正整数)则点P2015的坐标为( )A、(22014•
| ||||
B、(22012•
| ||||
C、(-22013•
| ||||
| D、(0,-22014) |
已知A(-1,y1),B(1,y2),C(2,y3)三点在抛物线y=x2-2x+m上,则y1、y2、y3的大小关系为( )
| A、y1<y2<y3 |
| B、y3<y2<y1 |
| C、y2<y1<y3 |
| D、y2<y3<y1 |
下列运算正确的是( )
| A、a5•a3=a15 |
| B、6a2m÷2am=3a2 |
| C、(-a5)2=a10 |
| D、a6÷a3=a2 |
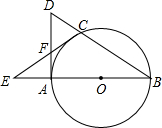 如图,AB是⊙O的直径,C是⊙O上的一点,过点A作DA⊥BA于点A,交BC的延长线于点D,延长BA至点E,连接CE交DA于点F,恰使AF=DF
如图,AB是⊙O的直径,C是⊙O上的一点,过点A作DA⊥BA于点A,交BC的延长线于点D,延长BA至点E,连接CE交DA于点F,恰使AF=DF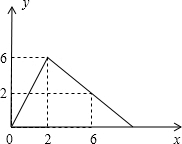 某医药研究所开发了一种新药,在实验药效时发现,如果成人按规定剂量服用,那么每毫升血液中含药量y(微克)随时间x(时)的变化情况如图所示,当成人按规定服药后:
某医药研究所开发了一种新药,在实验药效时发现,如果成人按规定剂量服用,那么每毫升血液中含药量y(微克)随时间x(时)的变化情况如图所示,当成人按规定服药后: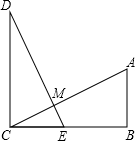 已知:如图,AB⊥BC,DC⊥BC,B、C分别是垂足,DE交AC于M,AC=DE,AB=EC,DE与AC有什么关系?请说明理由.
已知:如图,AB⊥BC,DC⊥BC,B、C分别是垂足,DE交AC于M,AC=DE,AB=EC,DE与AC有什么关系?请说明理由.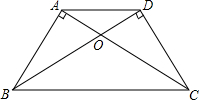 如图,AB⊥AC,DC⊥DB,填空:
如图,AB⊥AC,DC⊥DB,填空: 如图,AB=AC,AD=AE,∠BAC=∠DAE,∠1=21°,∠2=29°,则∠3=
如图,AB=AC,AD=AE,∠BAC=∠DAE,∠1=21°,∠2=29°,则∠3=