题目内容
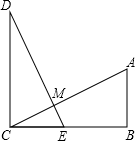 已知:如图,AB⊥BC,DC⊥BC,B、C分别是垂足,DE交AC于M,AC=DE,AB=EC,DE与AC有什么关系?请说明理由.
已知:如图,AB⊥BC,DC⊥BC,B、C分别是垂足,DE交AC于M,AC=DE,AB=EC,DE与AC有什么关系?请说明理由.考点:全等三角形的判定与性质
专题:
分析:求出∠DCE=∠B=90°,根据HL推出△DCE≌△CBA,根据全等三角形的性质得出DE=AC,∠D=∠ACB,求出∠DMC=90°即可.
解答:解:DE=AC,DE⊥AC,
理由是:∵AB⊥BC,DC⊥BC,
∴∠DCE=∠B=90°,
在Rt△DCE和Rt△CBA中
∴Rt△DCE≌Rt△CBA(HL),
∴DE=AC,∠D=∠ACB,
∵∠DCE=90°,
∴∠ACB+∠DCM=90°,
∴∠D+∠DCM=90°,
∴∠DMC=90°,
∴DE⊥AC.
理由是:∵AB⊥BC,DC⊥BC,
∴∠DCE=∠B=90°,
在Rt△DCE和Rt△CBA中
|
∴Rt△DCE≌Rt△CBA(HL),
∴DE=AC,∠D=∠ACB,
∵∠DCE=90°,
∴∠ACB+∠DCM=90°,
∴∠D+∠DCM=90°,
∴∠DMC=90°,
∴DE⊥AC.
点评:本题考查了全等三角形的性质和判定,三角形内角和定理的应用,解此题的关键是推出△DCE≌△CBA,注意:全等三角形的对应边相等,对应角相等.

练习册系列答案
相关题目
如图所示的标志中,不是轴对称图形的有( )
A、 |
B、 |
C、 |
D、 |
在Rt△ABC中,∠C=90°,AC=
AB,则cosA等于( )
| 1 |
| 3 |
A、
| ||||
B、
| ||||
C、2
| ||||
D、
|
下列各式y=2x、y=
、y=|x|-1、|y|=x、y=x2中y是x的函数的个数( )
| 1 |
| x |
| A、5 | B、4 | C、3 | D、2 |
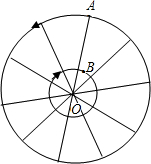 如图,一个同心圆圈的玩具,内外都等分成10格,都可绕着O点转动,若内圈按顺时针方向旋转,外圈按逆时针方向旋转,且内圈旋转的速度是外圈的4倍,当射线OB、OA按规定的方向同时转动:
如图,一个同心圆圈的玩具,内外都等分成10格,都可绕着O点转动,若内圈按顺时针方向旋转,外圈按逆时针方向旋转,且内圈旋转的速度是外圈的4倍,当射线OB、OA按规定的方向同时转动: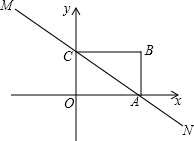 如图,直线MN与x轴,y轴分别相交于A、C两点,分别过A、C两点作x轴,y轴的乘线相交于B点,且OA,OC(OA>OC)的长分别是OC=6,OA=8
如图,直线MN与x轴,y轴分别相交于A、C两点,分别过A、C两点作x轴,y轴的乘线相交于B点,且OA,OC(OA>OC)的长分别是OC=6,OA=8 如图,反比例函数y=
如图,反比例函数y=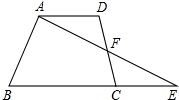 四边形ABCD中,AD∥BC,DF=CF,连接AF并延长交BC延长线于点E.
四边形ABCD中,AD∥BC,DF=CF,连接AF并延长交BC延长线于点E.