题目内容
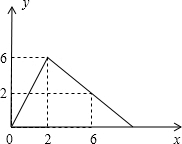 某医药研究所开发了一种新药,在实验药效时发现,如果成人按规定剂量服用,那么每毫升血液中含药量y(微克)随时间x(时)的变化情况如图所示,当成人按规定服药后:
某医药研究所开发了一种新药,在实验药效时发现,如果成人按规定剂量服用,那么每毫升血液中含药量y(微克)随时间x(时)的变化情况如图所示,当成人按规定服药后:(1)服药后
(2)服药后5小时,血液中含药量为每升
(3)当x≤2时,y与x之间的函数关系式是
(4)当x≥2时,y与x之间的函数关系式是
(5)如果每毫升血液中含药量3微克或3微克以上时,治疗疾病最有效,那么这个有效时间范围是
考点:一次函数的应用
专题:
分析:(1)由函数图象可以直接得出服药后2时,血液中含药量最高为每升6微克,而得出结论;
(2)设直线AB的解析式为y=kx+b,由待定系数法求出解析式,当x=5时代入解析式求出y的值即可;
(3)当x≤2时,设y与x之间的函数关系式y=k1x,由待定系数法求出其解即可;
(4)当x≥2时,y与x之间的函数关系式是y=kx+b,由待定系数法求出其解即可;
(5)当y=3时分别代入(3)、(4)的两个解析式求出x的值就可以求出结论.
(2)设直线AB的解析式为y=kx+b,由待定系数法求出解析式,当x=5时代入解析式求出y的值即可;
(3)当x≤2时,设y与x之间的函数关系式y=k1x,由待定系数法求出其解即可;
(4)当x≥2时,y与x之间的函数关系式是y=kx+b,由待定系数法求出其解即可;
(5)当y=3时分别代入(3)、(4)的两个解析式求出x的值就可以求出结论.
解答:解:(1)由函数图象,得
服药后2小时,血液中含药量最高为每升6微克.
故答案为:2,6;
(2)设直线AB的解析式为y=kx+b,由题意,得
,
解得:
,
∴y=-x+8,
当x=5时,y=3,
故答案为:3;
(3)当x≤2时,设y与x之间的函数关系式y=k1x,由题意,得
6=2k1,
解得:k1=3,
∴y=3x.
故答案为:y=3x;
(4)当x≥2时,y与x之间的函数关系式是y=kx+b,由题意,得
,
解得:
,
∴y=-x+8,
故答案为:y=-x+8;
(5)由题意,得
当y=3时,x=1或x=5,
∴有效时间范围是:5-1=4小时.
故答案为:4.
服药后2小时,血液中含药量最高为每升6微克.
故答案为:2,6;
(2)设直线AB的解析式为y=kx+b,由题意,得
|
解得:
|
∴y=-x+8,
当x=5时,y=3,
故答案为:3;
(3)当x≤2时,设y与x之间的函数关系式y=k1x,由题意,得
6=2k1,

解得:k1=3,
∴y=3x.
故答案为:y=3x;
(4)当x≥2时,y与x之间的函数关系式是y=kx+b,由题意,得
|
解得:
|
∴y=-x+8,
故答案为:y=-x+8;
(5)由题意,得
当y=3时,x=1或x=5,
∴有效时间范围是:5-1=4小时.
故答案为:4.
点评:本题考查了一次函数的图象的运用,待定系数法求一次函数的解析式的运用,由函数值求自变量的值的运用,由自变量的值求函数值的运用,解答时求出函数的解析式是关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
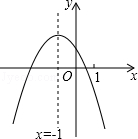 二次函数y=ax2+bx+c (a≠0)的图象如图,给出下列四个结论:
二次函数y=ax2+bx+c (a≠0)的图象如图,给出下列四个结论:①4ac-b2<0;②4a+c<2b;③3b+2c<0;④n(an+b)+b>a(n≠-1),
其中正确结论的个数是( )
| A、4个 | B、3个 | C、2个 | D、1个 |
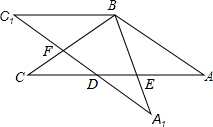 在△ABC中,AB=BC=4,∠ABC=120°,将△ABC绕点B旋转角α(0°<α<90°)得△A1BC1,A1B交AC于点E,A1C1分别交AC、BC于D、F两点.
在△ABC中,AB=BC=4,∠ABC=120°,将△ABC绕点B旋转角α(0°<α<90°)得△A1BC1,A1B交AC于点E,A1C1分别交AC、BC于D、F两点.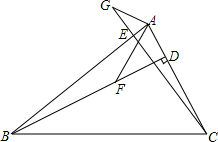 已知:BD,CE是△ABC的高,点F在BD上,BF=AC,点G在CE的延长线上,CG=AB.
已知:BD,CE是△ABC的高,点F在BD上,BF=AC,点G在CE的延长线上,CG=AB.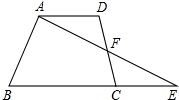 四边形ABCD中,AD∥BC,DF=CF,连接AF并延长交BC延长线于点E.
四边形ABCD中,AD∥BC,DF=CF,连接AF并延长交BC延长线于点E.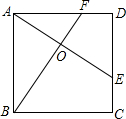 如图,E、F分别是正方形的边CD、AD上的点,且CE=DF,AE、BF交于点O,下列结论正确的个数为( )
如图,E、F分别是正方形的边CD、AD上的点,且CE=DF,AE、BF交于点O,下列结论正确的个数为( )