题目内容
4.如图1,在Rt△ABC中,∠ACB=90°,AC=6,BC=8,点D在边AB上运动,DE平分∠CDB交边BC于点E,EM⊥BD垂足为M,EN⊥CD垂足为N.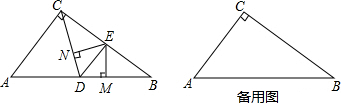
(1)当AD=CD时,求证:DE∥AC;
(2)探究:AD为何值时,以B,M,E为顶点的三角形与以C,E,N为顶点的三角形相似?
分析 (1)由等腰三角形的性质和角平分线的性质,得出∠DAC=∠BDE,即可证明DE∥AC.
(2)此题分两种情况求解,△BME∽△CNE或△BME∽△ENC,根据相似三角形的性质即可求得.
解答 (1)证明:∵AD=CD,
∴∠DAC=∠DCA,
∴∠BDC=2∠DAC,
又∵DE是∠BDC的平分线,
∴∠DAC=∠BDE,
∴DE∥AC;
(2)解:分两种情况:
①若△BME∽△CNE,必有∠MBE=∠NCE,
此时BD=DC,
∵DE平分∠BDC,
∴DE⊥BC,BE=EC,
又∵∠ACB=90°,
∴DE∥AC,
∴$\frac{BE}{BC}=\frac{BD}{AB}$即$BD=\frac{1}{2}AB=\frac{1}{2}\sqrt{A{C^2}+B{C^2}}=5$,
∴AD=5,
②若△BME∽△ENC,必有∠EBM=∠CEN,
此时NE∥ME,
∵CD⊥NE,
∴CD⊥AB,
∴AD=AC•cosA=AC•$\frac{AC}{AB}$=6×$\frac{6}{10}$=3.6,
∴当AD=5或AD=3.6时,以B,M,E为顶点的三角形与以C,E,N为顶点的三角形相似.
点评 此题考查了相似三角形的判定与性质、角平分线的性质和勾股定理,解题时要注意数形结合思想的应用,要注意不规则图形的面积的求解方法.

练习册系列答案
 导学全程练创优训练系列答案
导学全程练创优训练系列答案
相关题目
15.若分式$\frac{{x}^{2}-1}{x-1}$的值为0,则x的值为( )
| A. | 0 | B. | ±1 | C. | 1 | D. | -1 |
 一个三角形各顶点的坐标如图所示,把此三角形先向左平移3个单位长度,再向上平移2个单位长度得到三角形A′B′C′,
一个三角形各顶点的坐标如图所示,把此三角形先向左平移3个单位长度,再向上平移2个单位长度得到三角形A′B′C′,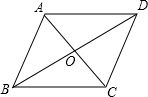 如图,平行四边形ABCD的对角线相交于O点,BC=14cm,BD=20cm,AC=12cm,则△AOD的周长为30cm.
如图,平行四边形ABCD的对角线相交于O点,BC=14cm,BD=20cm,AC=12cm,则△AOD的周长为30cm.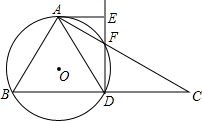 如图,在Rt△ABC中,斜边BC=12,∠C=30°,D为BC的中点,△ABD的外接圆⊙O与AC交于F点,过A作⊙O的切线AE交DF的延长线于E点.
如图,在Rt△ABC中,斜边BC=12,∠C=30°,D为BC的中点,△ABD的外接圆⊙O与AC交于F点,过A作⊙O的切线AE交DF的延长线于E点. 如图,⊙O的直径AB=6,点C为⊙0外一点,CA、CB分别交⊙O于E、F,cos∠C=$\frac{2}{3}$,则EF的长为( )
如图,⊙O的直径AB=6,点C为⊙0外一点,CA、CB分别交⊙O于E、F,cos∠C=$\frac{2}{3}$,则EF的长为( )