题目内容
18.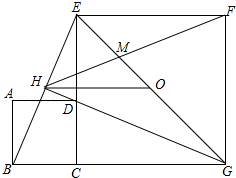 如图,正方形ABCD的边CD与正方形CEFG的边CE重合,点O是EG的中点,∠CGE的平分线GH过点D,交BE于H,连接OH、FH、EG与FH交于M,对于下面四个结论:
如图,正方形ABCD的边CD与正方形CEFG的边CE重合,点O是EG的中点,∠CGE的平分线GH过点D,交BE于H,连接OH、FH、EG与FH交于M,对于下面四个结论:①GH⊥BE;
②HO∥BG,HO=$\frac{1}{2}$BG;
③点H不在正方形CGFE的外接圆上;
④△GBE∽△GMF.
其中结论正确的个数是( )
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
分析 (1)由四边形ABCD和四边形CGFE是正方形,得出△BCE≌△DCG,推出∠BEC+∠HDE=90°,从而得GH⊥BE;
(2)由GH是∠EGC的平分线,得出△BGH≌△EGH,再由O是EG的中点,利用中位线定理,得HO∥BG,$HO=\frac{1}{2}BG$;
(3)△EHG是直角三角形,因为O为EG的中点,所以OH=OG=OE,得出点H在正方形CGFE的外接圆上;
(4)连接CF,由点H在正方形CGFE的外接圆上,得到∠HFC=∠CGH,由∠HFC+∠FMG=90°,∠CGH+∠GBE=90°,得出∠FMG=∠GBE,所以△GBE∽△GMF.
解答 解:(1)如图1,
∵四边形ABCD和四边形CGFE是正方形,
∴BC=CD,CE=CG,∠BCE=∠DCG,
在△BCE和△DCG中,
$\left\{\begin{array}{l}{BD=CD}\\{∠BCE=∠DCG}\\{CE=CG}\end{array}\right.$,
∴△BCE≌△DCG(SAS),
∴∠BEC=∠BGH,
∵∠BGH+∠CDG=90°,∠CDG=∠HDE,
∴∠BEC+∠HDE=90°,
∴GH⊥BE.
故①正确;
(2)∵GH是∠EGC的平分线,
∴∠BGH=∠EGH,
在△BGH和△EGH中,
$\left\{\begin{array}{l}{∠BGH=∠EGH}\\{GH=GH}\\{∠GHB=∠GHE}\end{array}\right.$,
∴△BGH≌△EGH(ASA),
∴BH=EH,
又∵O是EG的中点,
∴HO是△EBG的中位线,
∴HO∥BG,HO=$\frac{1}{2}$BG,
故②正确;
(3)由(1)得△EHG是直角三角形,
∵O为EG的中点,
∴OH=OG=OE,
∴点H在正方形CGFE的外接圆上,
故③错误;
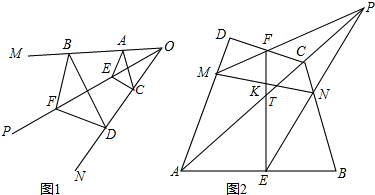
(4)如图2,连接CF,
由(3)可得点H在正方形CGFE的外接圆上,
∴∠HFC=∠CGH,
∵∠HFC+∠FMG=90°,∠CGH+∠GBE=90°,
∴∠FMG=∠GBE,
又∵∠EGB=∠FGM=45°,
∴△GBE∽△GMF.
故④正确,
故选:C.
点评 本题主要考查了四边形的综合题,解题的关键是能灵活利用三角形全等的判定和性质来解题.

| A. | 11.64亿 | B. | 11.64×108亿 | C. | 1.164×109亿 | D. | 116.4×107亿 |
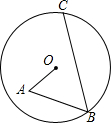 如图所示,⊙O内有折线OABC,其中OA=2,AB=4,∠A=∠B=60°,则BC的长为6.
如图所示,⊙O内有折线OABC,其中OA=2,AB=4,∠A=∠B=60°,则BC的长为6.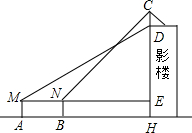 某电影上映前,一大型影院的楼顶挂起了一块广告牌CD.李老师目高MA=1.6m,他站在离大楼底部H点45m的A处测得大楼顶端点D的仰角为30°.接着他向大楼前进14m,站在B处,测得广告牌顶端C的仰角为45°.
某电影上映前,一大型影院的楼顶挂起了一块广告牌CD.李老师目高MA=1.6m,他站在离大楼底部H点45m的A处测得大楼顶端点D的仰角为30°.接着他向大楼前进14m,站在B处,测得广告牌顶端C的仰角为45°.