题目内容
9.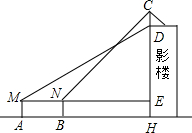 某电影上映前,一大型影院的楼顶挂起了一块广告牌CD.李老师目高MA=1.6m,他站在离大楼底部H点45m的A处测得大楼顶端点D的仰角为30°.接着他向大楼前进14m,站在B处,测得广告牌顶端C的仰角为45°.
某电影上映前,一大型影院的楼顶挂起了一块广告牌CD.李老师目高MA=1.6m,他站在离大楼底部H点45m的A处测得大楼顶端点D的仰角为30°.接着他向大楼前进14m,站在B处,测得广告牌顶端C的仰角为45°.(1)求这幢大楼的高DH;
(2)求这块广告牌CD的高度.
分析 首先分析图形:根据题意构造直角三角形Rt△DME与Rt△CNE;应利用ME-NE=AB=14构造方程关系式,进而可解即可求出答案.
解答 解:(1)在Rt△DME中,ME=AH=45m;
由tan30°=$\frac{DE}{ME}$,得DE=45×$\frac{\sqrt{3}}{3}$=15$\sqrt{3}$m;
又因为EH=MA=1.6m,
因而大楼DH=DE+EH=(15$\sqrt{3}$+$\frac{8}{5}$)m;
(2)又在Rt△CNE中,NE=45-14=31m,
由tan45°=$\frac{CE}{NE}$,得CE=NE=31m;
因而广告牌CD=CE-DE=(31-15$\sqrt{3}$)m;
答:楼高DH为(15$\sqrt{3}$+$\frac{8}{5}$)m,广告牌CD的高度为(31-15$\sqrt{3}$)m.
点评 本题要求学生借助仰角关系构造直角三角形,并结合图形利用三角函数解直角三角形.

练习册系列答案
相关题目
20.如果关于x的一元二次方程x2+px+q=0的两根分别为x1=-3,x2=2,那么p、q的值分别是( )
| A. | 1,-6 | B. | -1,-6 | C. | -1,6 | D. | 1,6 |
17.若3a=4b,则$\frac{a}{b}$=( )
| A. | $\frac{3}{4}$ | B. | $\frac{4}{3}$ | C. | $\frac{3}{2}$ | D. | $\frac{2}{3}$ |
14.在一个不透明的盒子里装着除颜色外完全相同的黑、白两种小球共40个.小颖做摸球实验.她将盒子里面的球搅匀后从中随机摸出一个球记下颜色后放回,不断重复上述过程,多次试验后,得到表中的数据数据,并得出了四个结论,其中正确的是( )
| 摸球的次数n | 100 | 200 | 300 | 500 | 800 | 1000 | 3000 |
| 摸到白球的次数m | 70 | 128 | 171 | 302 | 481 | 599 | 1806 |
| 摸到白球的频率$\frac{m}{n}$ | 0.75 | 0.64 | 0.57 | 0.604 | 0.601 | 0.599 | 0.602 |
| A. | 试验1500次摸到白球的频率比试验800次的更接近0.6 | |
| B. | 从该盒子中任意摸出一个小球,摸到白球的概率为0.6 | |
| C. | 当试验次数n为2000时,摸到白球的次数m一定等于1200 | |
| D. | 这个盒子中的白球定有28个 |
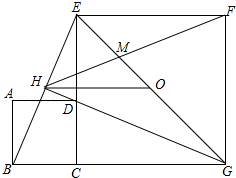 如图,正方形ABCD的边CD与正方形CEFG的边CE重合,点O是EG的中点,∠CGE的平分线GH过点D,交BE于H,连接OH、FH、EG与FH交于M,对于下面四个结论:
如图,正方形ABCD的边CD与正方形CEFG的边CE重合,点O是EG的中点,∠CGE的平分线GH过点D,交BE于H,连接OH、FH、EG与FH交于M,对于下面四个结论: