题目内容
11.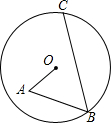 如图所示,⊙O内有折线OABC,其中OA=2,AB=4,∠A=∠B=60°,则BC的长为6.
如图所示,⊙O内有折线OABC,其中OA=2,AB=4,∠A=∠B=60°,则BC的长为6.
分析 延长AO交BC于D,根据∠A、∠B的度数易证得△ABD是等边三角形,由此可求出OD、BD的长;过O作BC的垂线,设垂足为E;在Rt△ODE中,根据OD的长及∠ODE的度数易求得DE的长,进而可求出BE的长;由垂径定理知BC=2BE,由此得解.
解答 解:延长AO交BC于D,作OE⊥BC于E,
∵∠A=∠B=60°,∴∠ADB=60°,
∴△ADB为等边三角形,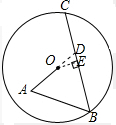
∴BD=AD=AB=4,
∴OD=2,又∵∠ADB=60°,
∴DE=$\frac{1}{2}$OD=1,
∴BE=3,
∴BC=2BE=6,
故答案为6.
点评 本题主要考查了等边三角形的判定和性质以及垂径定理的应用,构建合适的辅助线,数形结合,找出有关线段的关系,是解答此题的关键.

练习册系列答案
 优化作业上海科技文献出版社系列答案
优化作业上海科技文献出版社系列答案
相关题目
1.若函数y=(m-2)x的图象经过第二、四象限,则m的取值范围是( )
| A. | m>2 | B. | m<2 | C. | m≥2 | D. | m≤2 |
20.如果关于x的一元二次方程x2+px+q=0的两根分别为x1=-3,x2=2,那么p、q的值分别是( )
| A. | 1,-6 | B. | -1,-6 | C. | -1,6 | D. | 1,6 |
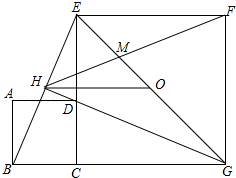 如图,正方形ABCD的边CD与正方形CEFG的边CE重合,点O是EG的中点,∠CGE的平分线GH过点D,交BE于H,连接OH、FH、EG与FH交于M,对于下面四个结论:
如图,正方形ABCD的边CD与正方形CEFG的边CE重合,点O是EG的中点,∠CGE的平分线GH过点D,交BE于H,连接OH、FH、EG与FH交于M,对于下面四个结论: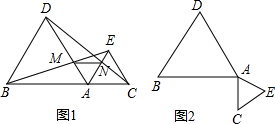
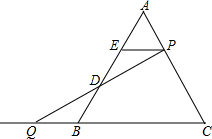 如图,△ABC是等边三角形,P是AC边上任意一点(与A、C两点不重合),Q是CB延长线上一点,且始终满足条件BQ=AP,过P作PE∥BC交AB于点E,连接PQ交AB于D.
如图,△ABC是等边三角形,P是AC边上任意一点(与A、C两点不重合),Q是CB延长线上一点,且始终满足条件BQ=AP,过P作PE∥BC交AB于点E,连接PQ交AB于D.