题目内容
 如图,△ABC是等边三角形,D是AB边上的一点,以CD为边作等边三角形CDE,使点E、A在直线DC的同侧,连结AE,求证:BD=AE.
如图,△ABC是等边三角形,D是AB边上的一点,以CD为边作等边三角形CDE,使点E、A在直线DC的同侧,连结AE,求证:BD=AE.考点:全等三角形的判定与性质,等边三角形的性质
专题:证明题
分析:根据等边三角形性质推出BC=AC,CD=CE,∠ABC=∠BCA=∠ECD=60°,求出∠BCD=∠ACE,根据SAS证△ACE≌△BCD,即可证明BD=AE.
解答:证明:∵△ABC和△DEC是等边三角形,
∴BC=AC,CD=CE,∠ABC=∠BCA=∠ECD=60°,
∴∠BCA-∠DCA=∠ECD-∠DCA,
即∠BCD=∠ACE,
在△ACE和△BCD中,
,
∴△ACE≌△BCD(SAS),
∴BD=AE.
∴BC=AC,CD=CE,∠ABC=∠BCA=∠ECD=60°,
∴∠BCA-∠DCA=∠ECD-∠DCA,
即∠BCD=∠ACE,
在△ACE和△BCD中,
|
∴△ACE≌△BCD(SAS),
∴BD=AE.
点评:本题考查了等边三角形性质,全等三角形的判定和性质,关键是证明△ACE≌△BCD是解题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
如图,将半径为3的圆形纸片,按下列顺序折叠,若
和
都经过圆心O,则阴影部分的面积是( )

 |
| AB |
 |
| BC |

| A、π | B、2π | C、3π | D、4π |
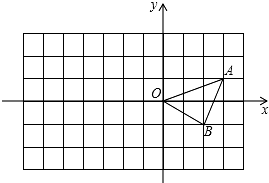 如图,已知O是坐标原点,A、B的坐标分别为(3,1),(2,-1).
如图,已知O是坐标原点,A、B的坐标分别为(3,1),(2,-1).