题目内容
10．（1）计算：$\sqrt{9}$-$\root{3}{-27}$+22（2）因式分解：x3-4x．
分析 （1）原式第一项利用算术平方根定义计算，第二项利用立方根定义计算，最后一项利用乘方的意义化简，计算即可得到结果；
（2）原式提取x，再利用平方差公式分解即可．
解答 解：（1）原式=3-（-3）+4=3+3+4=10；
（2）原式=x（x2-4）=x（x+2）（x-2）．
点评 此题考查了实数的运算，以及提公因式法与公式法的综合运用，熟练掌握运算法则是解本题的关键．
练习册系列答案
相关题目
20．下列各式计算正确的是（ ）
| A． | 2+$\sqrt{3}$=2$\sqrt{3}$ | B． | 2x-2=$\frac{1}{2{x}^{2}}$ | C． | 3a2•2a3=6a6 | D． | a8÷a2=a6 |
1．
如图，已知AB∥CD，CE交AB于点F，若∠E=20°，∠C=45°，则∠A的度数为（ ）
如图，已知AB∥CD，CE交AB于点F，若∠E=20°，∠C=45°，则∠A的度数为（ ）| A． | 5° | B． | 15° | C． | 25° | D． | 35° |
如图，一艘轮船位于灯塔P的北偏东45°方向，距灯塔100海里的A处，它沿正南方向航行一段时间后，到达位于灯塔P的南偏东35°方向上的B处．这时，轮船所在的B处距离灯塔P有多远？（精确到0.1海里）（参考数据：$\sqrt{2}$≈1.41，$\sqrt{3}$≈1.73，sin35°≈0.57，cos35°≈0.82，tan35°≈0.70）
5．对于一组统计数据：3，4，2，2，4，下列说法错误的是（ ）
| A． | 中位数是3 | B． | 平均数是3 | C． | 方差是0.8 | D． | 众数是4 |
15．已知方程组$\left\{\begin{array}{l}{a_1}x+{b_1}y={c_1}\\{a_2}x+{b_2}y={c_2}\end{array}\right.$的解是$\left\{\begin{array}{l}x=5\\ y=10\end{array}\right.$；则关于x，y的方程组$\left\{\begin{array}{l}{a_1}x-{b_1}y={a_1}+{c_1}\\{a_2}x-{b_2}y={a_2}+{c_2}\end{array}\right.$的解是（ ）
| A． | $\left\{\begin{array}{l}x=6\\ y=10\end{array}\right.$ | B． | $\left\{\begin{array}{l}x=6\\ y=-10\end{array}\right.$ | C． | $\left\{\begin{array}{l}x=-6\\ y=10\end{array}\right.$ | D． | $\left\{\begin{array}{l}x=-6\\ y=-10\end{array}\right.$ |
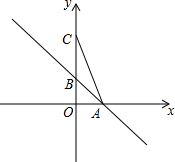如图，一次函数y=-x+1的图象与x轴、y轴分别交于点A、B．点C在y轴的正半轴上，且sin∠ACB=$\frac{\sqrt{10}}{10}$ 
如图，射线AB，CD分别与直线l相交于点G、H，若∠1=∠2，∠C=65°，则∠A的度数是115°．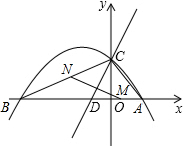
已知抛物线y=ax2+bx+c（a＜0）与x轴交于点A（8，0）和B（-12，0），与y轴交于点C（0，6）．