题目内容
2.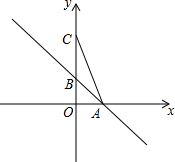 如图,一次函数y=-x+1的图象与x轴、y轴分别交于点A、B.点C在y轴的正半轴上,且sin∠ACB=$\frac{\sqrt{10}}{10}$
如图,一次函数y=-x+1的图象与x轴、y轴分别交于点A、B.点C在y轴的正半轴上,且sin∠ACB=$\frac{\sqrt{10}}{10}$ (1)求点C的坐标;
(2)在直线AB上有一点D,若满足∠CDB=∠ACB,求BD的长.
分析 (1)根据一次函数图象的点的坐标得出OA=1,利用三角函数即可得出OC的长度,得出坐标即可;
(2)分当点D在AB的延长线时和当点D在BA的延长线上时两种情况进行分析解答.
解答 解:(1)∵一次函数y=-x+1,
∴OA=1,
在Rt△OAC中,
∵sin∠ACB=$\frac{\sqrt{10}}{10}$,
∴OC=3,
即C的坐标为(0,3);
(2)①当点D在AB的延长线时,过点C作CE⊥AB于点E,如图1: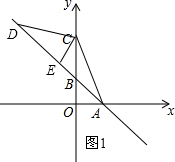
由直线AB表达式可得:OB=1,∠ABO=45°,
∴BC=2,∠CBE=45°,
在Rt△CBE中,可得:CE=BE=$\sqrt{2}$,BC=2,
在Rt△CDE中,
∵sin∠CDE=$\frac{\sqrt{10}}{10}$,
∴DE=3CE=3$\sqrt{2}$,
∴BD=BE+ED=4$\sqrt{2}$;
②当点D在BA的延长线上时,如图2: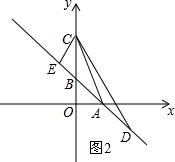
由对称性可知,DE=3$\sqrt{2}$,
∴BD=DE-BE=2$\sqrt{2}$.
点评 此题考查一次函数点的坐标,关键是根据一次函数图象的性质得出其点的坐标.

练习册系列答案
相关题目
13.用科学记数法表示0.0000907的结果正确的是( )
| A. | 9.1×10-4 | B. | 9.1×10-5 | C. | 9.0×10-5 | D. | 9.07×10-5 |
17.二次函数y=ax2+bx+c(a,b,c为常数,且a≠0)中的x与y的部分对应值如表:
下列结论:(1)ac<0;(2)当x>1时,y的值随x值的增大而减小.(3)3是方程ax2+(b-1)x+c=0的一个根;(4)当-1<x<3时,ax2+(b-1)x+c>0.其中正确的个数为( )
| x | … | -1 | 0 | 1 | 3 | … |
| y | … | -1 | 3 | 5 | 3 | … |
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
14.统计甲乙两人各10次射击的成绩发现,两人10次射击的平均成绩一样高,方差分别为S甲2=2,S乙2=5,则两人这10次射击成绩比较稳定的是( )
| A. | 甲 | B. | 乙 | C. | 两者一样稳定 | D. | 无法判断 |
 如图,四边形ABCD内接于⊙O,AB=AD,∠C=110°,点E在$\widehat{AD}$上,则∠E=125°.
如图,四边形ABCD内接于⊙O,AB=AD,∠C=110°,点E在$\widehat{AD}$上,则∠E=125°.