题目内容
20.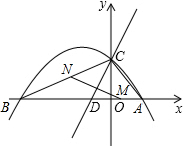 已知抛物线y=ax2+bx+c(a<0)与x轴交于点A(8,0)和B(-12,0),与y轴交于点C(0,6).
已知抛物线y=ax2+bx+c(a<0)与x轴交于点A(8,0)和B(-12,0),与y轴交于点C(0,6).(1)求该抛物线的解析式:
(2)点D在线段AB上且AD=AC,若动点M从A出发沿线段AB以每秒1个单位长度的速度匀速运动,同时另一动点N以某一速度从B出发沿线段BC匀速运动,问是否存在某一时刻t(秒),使线段MN被直线CD垂直平分?若存在,请求出此时的时间t和点N的运动速度;若不存在,请说明理由;
(3)在第二象限的抛物线上取一点P,使得S△PCA=S△PCB,再在抛物线上找一点Q(不与点A、B、C重合),使得tan∠PBQ=$\frac{1}{2}$,求点Q的坐标.
分析 (1)由抛物线y=ax2+bx+c(a<0)与x轴交于点A(8,0)和B(-12,0),可设抛物线的解析式为y=a(x-8)(x+12),再把C的坐标代入抛物线解析式,求出a的值即可;
(2)由AD=AC=10,求出点D的坐标是(-2,0),于是BD=AD.若CD垂直平分MN,根据线段垂直平分线的性质和等腰三角形的性质得出DN=DM,∠NDC=∠MDC=∠ACD,那么DN∥AC,BN=CN,DN是△ABC的中位线,根据三角形中位线定理得出DN=$\frac{AC}{2}$=5,所以AM=t=5,再求出BN=5VN=3$\sqrt{5}$,根据速度=路程÷时间,计算即可求出N的运动速度;
(3)由S△PCA=S△PCB,根据三角形的面积公式可知A、B到PC的距离相等,于是PC∥AB,那么P(-4,6).由tan∠PBQ=$\frac{1}{2}$=tan∠CBA,得出∠PBQ=∠CBA,于是∠PBC=∠QBA.作PG⊥BC于G,QH⊥AB于H,求出PG=$\frac{4\sqrt{5}}{5}$,CG=$\frac{8\sqrt{5}}{5}$,BG=$\frac{22\sqrt{5}}{5}$,则tan∠PBC=$\frac{PG}{BG}$=$\frac{2}{11}$,Q(x,-$\frac{1}{16}$x2-$\frac{1}{4}$x+6),由tan∠QBA=tan∠PBC列出方程,解方程即可.
解答 解:(1)∵抛物线y=ax2+bx+c(a<0)与x轴交于点A(8,0)和B(-12,0),
∴可设抛物线的解析式为y=a(x-8)(x+12),
又∵抛物线过点C(0,6),
∴6=-96a,解得a=-$\frac{1}{16}$,
∴y=-$\frac{1}{16}$(x-8)(x+12)=-$\frac{1}{16}$x2-$\frac{1}{4}$x+6,
即该抛物线的解析式为y=-$\frac{1}{16}$x2-$\frac{1}{4}$x+6; (2)∵A(8,0),C(0,6),
(2)∵A(8,0),C(0,6),
∴AC=$\sqrt{{8}^{2}+{6}^{2}}$=10,
∴AD=AC=10,
∴点D的坐标是(-2,0),
∵B(-12,0),
∴BD=AD.
若CD垂直平分MN,则DN=DM,∠NDC=∠MDC=∠ACD,
∴DN∥AC,
∴BN=CN,
∴DN是△ABC的中位线,DN=$\frac{AC}{2}$=5,
∴AM=t=5,
而BN=5VN=3$\sqrt{5}$,点N的运动速度是$\frac{3\sqrt{5}}{5}$;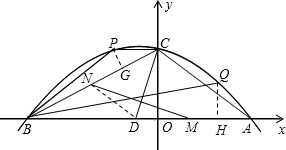 (3)∵S△PCA=S△PCB,
(3)∵S△PCA=S△PCB,
∴A、B到PC的距离相等,
∴PC∥AB,
∴P、C关于抛物线y=-$\frac{1}{16}$x2-$\frac{1}{4}$x+6的对称轴x=-2对称,
∵C(0,6),
∴P(-4,6).
∵tan∠PBQ=$\frac{1}{2}$,tan∠CBA=$\frac{OC}{OB}$=$\frac{6}{12}$=$\frac{1}{2}$,
∴∠PBQ=∠CBA,
∴∠PBQ-∠CBQ=∠CBA-∠CBQ,即∠PBC=∠QBA.
作PG⊥BC于G,QH⊥AB于H.
∵PG=$\frac{PC•OC}{BC}$=$\frac{4×6}{6\sqrt{5}}$=$\frac{4\sqrt{5}}{5}$,
CG=$\sqrt{P{C}^{2}-P{G}^{2}}$=$\sqrt{{4}^{2}-(\frac{4\sqrt{5}}{5})^{2}}$=$\frac{8\sqrt{5}}{5}$,
BG=BC-CG=6$\sqrt{5}$-$\frac{8\sqrt{5}}{5}$=$\frac{22\sqrt{5}}{5}$,
∴tan∠PBC=$\frac{PG}{BG}$=$\frac{\frac{4\sqrt{5}}{5}}{\frac{22\sqrt{5}}{5}}$=$\frac{2}{11}$.
设点Q的坐标为(x,-$\frac{1}{16}$x2-$\frac{1}{4}$x+6),
∵tan∠QBA=tan∠PBC,
∴$\frac{-\frac{1}{16}{x}^{2}-\frac{1}{4}x+6}{x+12}$=$\frac{2}{11}$,
解得x=$\frac{56}{11}$或-12(舍去),
故点Q的坐标是($\frac{56}{11}$,$\frac{376}{121}$).
点评 本题是二次函数的综合题,考查了待定系数法求二次函数的解析式,线段垂直平分线的性质,等腰三角形的性质,平行线的判定和性质,三角形中位线定理,三角形的面积,锐角三角函数,勾股定理等知识,熟练掌握性质定理以及求解析式的方法是解题的关键.

 口算题卡北京妇女儿童出版社系列答案
口算题卡北京妇女儿童出版社系列答案 如图,四边形ABCD内接于⊙O,AB=AD,∠C=110°,点E在$\widehat{AD}$上,则∠E=125°.
如图,四边形ABCD内接于⊙O,AB=AD,∠C=110°,点E在$\widehat{AD}$上,则∠E=125°.
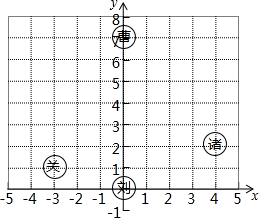 三国时期的一次战役中,曹军的位置在(0,7),蜀军的3支部队位置如图所示,诸葛亮安排关羽先向北然后向东移动刘备向北移动,张飞先向北再向西移动,从三面围击曹军.
三国时期的一次战役中,曹军的位置在(0,7),蜀军的3支部队位置如图所示,诸葛亮安排关羽先向北然后向东移动刘备向北移动,张飞先向北再向西移动,从三面围击曹军.