题目内容
8．
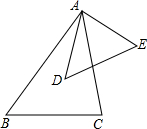如图，∠BAD=∠CAE，∠B=∠D．（1）△ABC和△ADE相似吗？为什么？
（2）如果AB=2AD，BC=4，那么DE的长度为多少？
分析 （1）根据已知得出∠BAC=∠DAE，进而得出△ADE∽△ABC；
（2）由△ADE∽△ABC，得到比例式，代入数值即可求得结果．
解答 解：（1）△ABC和△ADE相似，
理由：∵∠BAD=∠CAE，
∴∠BAD+∠DAC=∠CAE+∠DAC，
∴∠BAC=∠DAE，
∵∠B=∠D，
∴△ABC∽△ADE；
（2）∵△ABC∽△ADE，
∴$\frac{AB}{AD}$=$\frac{BC}{BE}$=$\frac{2}{1}$，
∵BC=4，
∴DE=2．
点评 此题主要考查了相似三角形的判定与性质，根据已知得出△ADE∽△ABC是解决问题的关键．
练习册系列答案
相关题目
17．甲、乙两组数据（单位：厘米）如下表
（1）根据以上数据填表（参考公式：S2=$\frac{1}{n}$[（x1-$\overline{x}$）2+（x2-$\overline{x}$）2+…+（xn-$\overline{x}$）2]）
（2）那一组数据比较稳定？
| 甲组 | 173 | 172 | 174 | 172 | 174 |
| 乙组 | 173 | 174 | 172 | 173 | 173 |
| 众数（单位：厘米） | 平均数（单位：厘米） | 方差（单位：厘米） | |
| 甲组 | 172 | 173 | 0.8 |
| 乙组 | 173 | 173 | 0.4 |
如图，∠ACB=90°，D为AB的中点，连接DC并延长到E，使CE=$\frac{1}{3}$CD，过点B作BF∥DE，与AE的延长线交于点F．若AB=6，则BF的长为8．
如图，AB与CD相交于点O，且AC∥BD．求证：OA•OD=OC•OB．
如图：把一个矩形如图折叠，使顶点B和D重合，折痕为EF．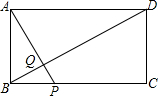
如图，矩形ABCD中，AB=4，BC=10，点P为BC边上一动点，AP交BD于点Q．点P从B点出发沿BC边以每秒1个单位长度的速度向C点移动，移动时间为t秒．