题目内容
12.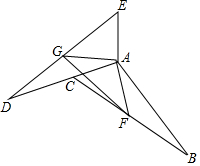 如图,把△ABC绕点A顺时针旋转n度(0<n<180)后得到△ADE,并使点D落在AC的延长线上.
如图,把△ABC绕点A顺时针旋转n度(0<n<180)后得到△ADE,并使点D落在AC的延长线上.(1)若∠B=17°,∠E=55°,求n;
(2)若F为BC的中点,G为DE的中点,连AG、AF、FG,求证:△AFG为等腰三角形.
分析 (1)根据旋转的性质得到∠ACB=∠E=55°,根据三角形的内角和得到∠BAC=180°-55°-17°=108°,于是得到结论;
(2)根据旋转的性质得到AB=AD BC=DE,∠B=∠D,根据线段中点的定义得到BF=$\frac{1}{2}$BC DG=$\frac{1}{2}$DE,根据全等三角形的性质即可得到结论.
解答 解:(1)∵△ADE是由△ABC旋转而来,
∴∠ACB=∠E=55°,
又∵∠B=17°,
∴∠BAC=180°-55°-17°=108°,
∵D落在AC延长线上,
∴∠BAC即为旋转角,
∴n=108°;
(2)证明:∵△ADE是由△ABC旋转而来,
∴AB=AD BC=DE,∠B=∠D,
∵F、G分别是BC、DE的中点,
∴BF=$\frac{1}{2}$BC DG=$\frac{1}{2}$DE,
∴BF=DG,
在△ABF与△ADG中$\left\{\begin{array}{l}AB=AD\\∠ABF=∠ADG\\ BF=DG\end{array}\right.$,
∴△ABF≌△ADG(SAS),
∴AF=AG,
∴△ADF是等腰三角形.
点评 本题考查了旋转的性质,全等三角形的判断和性质,等腰三角形的性质和判定,熟练掌握各知识点是解题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
3.若关于x的一元二次方程(m-2)x2+5x+m2-3m+2=0有一根为0,则m值为( )
| A. | 1 | B. | 0 | C. | 1或2 | D. | 2 |
7.关于x的方程kx2+(1-k)x-1=0有实数根,则k的取值范围是( )
| A. | k≠0 | B. | k为一切实数 | C. | k≥-$\frac{1}{2}$且k≠0 | D. | k≥-$\frac{1}{2}$ |
 如图,点D是△ABC内一点,已知∠ABD=20°,∠BDC=90°,∠ACD=30°,则∠A=40°度.
如图,点D是△ABC内一点,已知∠ABD=20°,∠BDC=90°,∠ACD=30°,则∠A=40°度.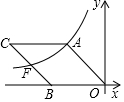 如图,O为坐标原点,四边形OACB是菱形,点B在x轴的负半轴上,sin∠AOB=$\frac{4}{5}$,反比例函数y=$\frac{k}{x}$在第二象限内的图象经过点A,与BC交于点F,若△AOF的面积为20,则该反比例函数的表达式为y=$\frac{24}{x}$.
如图,O为坐标原点,四边形OACB是菱形,点B在x轴的负半轴上,sin∠AOB=$\frac{4}{5}$,反比例函数y=$\frac{k}{x}$在第二象限内的图象经过点A,与BC交于点F,若△AOF的面积为20,则该反比例函数的表达式为y=$\frac{24}{x}$.