题目内容
17．
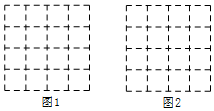如图，正方形网格中的每个小正方形的边长都是1，每个小格的顶点叫做格点．（1）在图1中以格点为顶点画一个面积为10的正方形；
（2）①在图2中以格点为顶点画一个三角形，使三角形三边长分别为$\sqrt{5}$、2$\sqrt{5}$、5；
②求：此三角形最长边上的高．
分析 （1）首先得出正方形的边长，进而得出答案；
（2）①利用勾股定里得出符合题意的答案；
②首先得出三角形的形状，再利用直角三角形面积得出答案．
解答 
解：（1）如图所示：正方形即为所求；
（2）①如图所示：三角形三边长分别为$\sqrt{5}$、2$\sqrt{5}$、5；
②设此三角形最长边上的高为x，
∵（$\sqrt{5}$）2+（2$\sqrt{5}$）2=5+20=25，
52=25，
∴此三角形是直角三角形；
则由三角形面积可得：$\sqrt{5}$×2$\sqrt{5}$=5x，
解得：x=2．
点评 此题主要考查了应用设计与作图以及勾股定理，正确应用勾股定理是解题关键．
练习册系列答案
相关题目
将一直角三角板与两边平行的纸条如图放置．已知∠1=30°，则∠2=60°．
12．
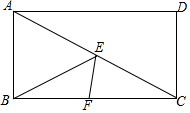如图，在矩形ABCD中，AB=2，BC=4，点E和点F分别是AC和BC上的动点，在点E和点F运动的过程中，BE+EF的最小值为（ ）
如图，在矩形ABCD中，AB=2，BC=4，点E和点F分别是AC和BC上的动点，在点E和点F运动的过程中，BE+EF的最小值为（ ）| A． | $\frac{16}{5}$ | B． | $\frac{8}{5}$ | C． | $\frac{8\sqrt{5}}{5}$ | D． | $\frac{2\sqrt{5}}{5}$ |
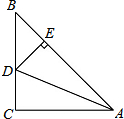如图，在△ABC中，∠C=90°，AC=BC，AD平分∠BAC交BC于点D，DE⊥AB于点E，若△BDE的周长是5cm，则AB的长为5cm．
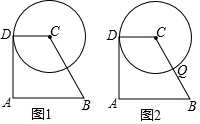如图1，四边形ABCD中，AB∥CD，AB=2CD=2$\sqrt{3}$，AD=3，⊙C与AD相切于点D，P是线段AB上一动点，以点P为圆心，PB长为半径作⊙P．
7．关于x的方程kx2+（1-k）x-1=0有实数根，则k的取值范围是（ ）
| A． | k≠0 | B． | k为一切实数 | C． | k≥-$\frac{1}{2}$且k≠0 | D． | k≥-$\frac{1}{2}$ |