题目内容
10.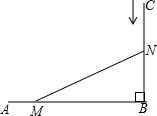 如图所示,AB⊥CB,AB=10cm,BC=8cm.一只螳螂由A点以每秒2cm的速度由A向B爬行,与此同时,一口蝉从C点以每秒1cm的速度由C向B爬行,当螳螂和蝉爬行x秒后,它们分别到达了点M,N的位置,此时,△MNB的面积恰好为24cm2.根据题意可得方程( )
如图所示,AB⊥CB,AB=10cm,BC=8cm.一只螳螂由A点以每秒2cm的速度由A向B爬行,与此同时,一口蝉从C点以每秒1cm的速度由C向B爬行,当螳螂和蝉爬行x秒后,它们分别到达了点M,N的位置,此时,△MNB的面积恰好为24cm2.根据题意可得方程( )| A. | 2x•x=24 | B. | (10-2x)(8-x)=24 | C. | (10-x)(8-2x)=24 | D. | (10-2x)(8-x)=48 |
分析 分别表示出螳螂和蝉爬行的距离后表示出MB和NB的值,利用三角形的面积公式计算即可.
解答 解:根据题意得:AM=2xcm,CN=xcm,
则MB=(10-2x)cm,NB=(8-x)cm,
∵△MNB的面积恰好为24cm2,
∴$\frac{1}{2}$(10-2x)(8-x)=24,
即:(10-2x)(8-x)=48,
故选D.
点评 本题考查了由实际问题抽象出一元二次方程的知识,解题的关键是能够分别表示出线段MB和线段NB的长,难度不大.

练习册系列答案
相关题目
1.估计$2\sqrt{6}-1$的值在( )
| A. | 2与3之间 | B. | 3与4之间 | C. | 4与5之间 | D. | 5与6之间 |
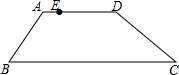 如图,四边形ABCD是梯形,AD∥BC,E为AD上任意一点,∠B+∠C=90°,请先将AB向右平移,使点A与点E重合,交BC于点F,再将CD向作平移,使点D与点E重合,交BC于点G,画出平移后的图形,并判断△EFG的形状.
如图,四边形ABCD是梯形,AD∥BC,E为AD上任意一点,∠B+∠C=90°,请先将AB向右平移,使点A与点E重合,交BC于点F,再将CD向作平移,使点D与点E重合,交BC于点G,画出平移后的图形,并判断△EFG的形状.
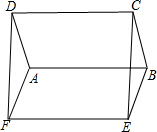 如图,?ABCD与?ABEF中,BC=BE,∠ABC=∠ABE,求证:四边形EFDC是矩形.
如图,?ABCD与?ABEF中,BC=BE,∠ABC=∠ABE,求证:四边形EFDC是矩形.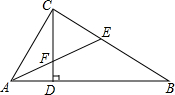 如图所示,在△ABC中,∠ACB=90°,高CD和角平分线AE交于点F,求证:CF=CE.
如图所示,在△ABC中,∠ACB=90°,高CD和角平分线AE交于点F,求证:CF=CE.